力扣第 2123 题
题目
给你一个 下标从 0 开始 的矩阵 grid。每次操作,你可以把 grid 中的 一个 1 变成 0 。
如果一个矩阵中,没有 1 与其它的 1 四连通(也就是说所有 1 在上下左右四个方向上不能与其他 1 相邻),那么该矩阵就是 完全独立 的。
请返回让 grid 成为 完全独立 的矩阵的 最小操作数。
示例 1:
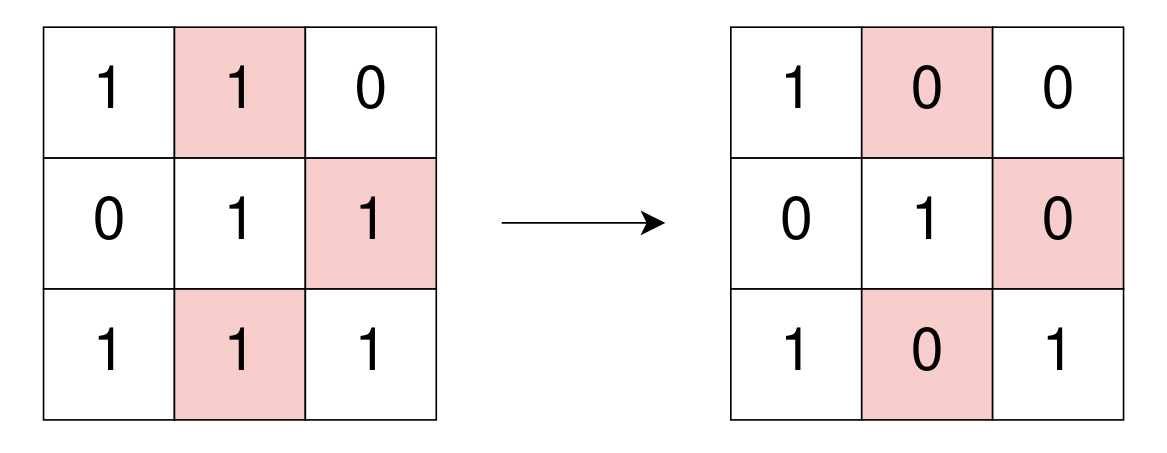
输入: grid = [[1,1,0],[0,1,1],[1,1,1]]
输出: 3
解释: 可以进行三次操作(把 grid[0][1], grid[1][2] 和 grid[2][1] 变成 0)。
操作后的矩阵中的所有的 1 与其它 1 均不相邻,因此矩阵是完全独立的。
示例 2:
输入: grid = [[0,0,0],[0,0,0],[0,0,0]]
输出: 0
解释: 矩阵中没有 1,此时矩阵也是完全独立的,因此无需操作,返回 0。
示例 3:
输入: grid = [[0,1],[1,0]]
输出: 0
解释: 矩阵中的所有的 1 与其它 1 均不相邻,已经是完全独立的,因此无需操作,返回 0。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j] 是 0 或者 1.
相似问题:
分析
- 相邻的 1 连边,即是二分图(按i+j的奇偶性分为两边)
- 问题转为求最小点覆盖,即是最大匹配数,可以用网络流解决
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
# 最大流 dinic
class MF:
def __init__(self,N):
self.g = [[] for _ in range(N)] # g 是图中每个 u 对应的 v 列表
self.d = [inf]*N # d 是图中每个 u 离源点 s 的最小距离
self.p = [0]*N # p 是当前弧优化,跳过已增广的边
self.N = N
def add(self,u,v,c): # 顶点 u 和 v 连边,容量 c
self.g[u].append([v,len(self.g[v]),c])
self.g[v].append([u,len(self.g[u])-1,0])
def bfs(self,s,t): # bfs 得到层次图
self.d = [inf]*self.N
self.d[s] = 0
dq = deque([s])
while dq:
u = dq.popleft()
for v,_,c in self.g[u]:
if c>0 and self.d[v]==inf:
dq.append(v)
self.d[v]=self.d[u]+1
return self.d[t]<inf
def dfs(self,u,t,flow): # dfs 得到阻塞流,多路增广+当前弧优化
if u==t:
return flow
res = 0
for i in range(self.p[u],len(self.g[u])):
self.p[u] += 1
v,j,c = self.g[u][i]
if c>0 and self.d[v]==self.d[u]+1:
a = self.dfs(v,t,min(flow,c))
flow -= a
self.g[u][i][-1] -= a
self.g[v][j][-1] += a
res += a
if flow==0:
break
return res
def cal(self,s,t): # 重复增广,计算最大流
res = 0
while self.bfs(s,t):
self.p = [0]*self.N
res += self.dfs(s,t,inf)
return res
class Solution:
def minimumOperations(self, grid: List[List[int]]) -> int:
m,n = len(grid),len(grid[0])
s,t = m*n,m*n+1
mf = MF(m*n+2)
for i in range(m):
for j in range(n):
if grid[i][j]==1:
u = i*n+j
if (i+j)%2:
mf.add(s,u,1)
else:
mf.add(u,t,1)
for x,y in [(i-1,j),(i,j-1)]:
if 0<=x<m and 0<=y<n and grid[x][y]==1:
v = x*n+y
if (i+j)%2:
mf.add(u,v,1)
else:
mf.add(v,u,1)
return mf.cal(s,t)
|
1622 ms


