1284：转化为全零矩阵的最少反转次数（1810 分）

Ian

2019-12-08 约 667 字预计阅读 2 分钟次阅读

力扣第 166 场周赛第 4 题

题目

给你一个 m x n 的二进制矩阵 mat。每一步，你可以选择一个单元格并将它反转（反转表示 0 变 1 ，1 变 0 ）。如果存在和它相邻的单元格，那么这些相邻的单元格也会被反转。相邻的两个单元格共享同一条边。

请你返回将矩阵 mat 转化为全零矩阵的最少反转次数，如果无法转化为全零矩阵，请返回 -1 。

二进制矩阵 的每一个格子要么是 0 要么是 1 。

全零矩阵 是所有格子都为 0 的矩阵。

示例 1：

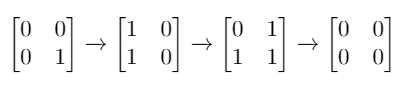
输入：mat = [[0,0],[0,1]]
输出：3
解释：一个可能的解是反转 (1, 0)，然后 (0, 1) ，最后是 (1, 1) 。

示例 2：

输入：mat = [[0]]
输出：0
解释：给出的矩阵是全零矩阵，所以你不需要改变它。

示例 3：

输入：mat = [[1,0,0],[1,0,0]]
输出：-1
解释：该矩阵无法转变成全零矩阵

提示：

m == mat.length
n == mat[0].length
1 <= m <= 3
1 <= n <= 3
mat[i][j] 是 0 或 1 。

相似问题：

分析

#1

把整个矩阵看作状态，即是典型的 bfs

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution:
    def minFlips(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        st = sum(mat[i][j]<<(i*n+j) for i in range(m) for j in range(n))
        Q, vis = deque([(0,st)]), {st}
        while Q:
            w,st = Q.popleft()
            if st==0:
                return w
            for i,j in product(range(m),range(n)):
                st2 = st
                st2 ^= 1<<(i*n+j)
                for x,y in [(i+1,j),(i,j+1),(i-1,j),(i,j-1)]:
                    if 0<=x<m and 0<=y<n:
                        st2 ^= 1<<(x*n+y)
                if st2 not in vis:
                    Q.append((w+1,st2))
                    vis.add(st2)
        return -1

7 ms

#2

还有更优的做法

注意到只要确定了第一行翻转哪些格子，为了保证全零，后面的都只有一种选法
因此，枚举第一行翻转的子集，确定后面的翻转格子，判断能否全零即可
m 比 n 小时，可以转置矩阵，节省时间

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


class Solution:
    def minFlips(self, mat: List[List[int]]) -> int:
        m,n = len(mat), len(mat[0])
        if m<n:
            m,n,mat = n,m,list(zip(*mat))
        A = [sum(row[j]<<j for j in range(n)) for row in mat]
        res = inf
        for st in range(1<<n):
            s,a,b = 0,0,st
            for x in A:
                s += b.bit_count()
                a,b = b,x^a^b^(b>>1)^((b<<1)%(1<<n))
            if b==0 and s<res:
                res = s
        return res if res<inf else -1 

0 ms

目录

1284：转化为全零矩阵的最少反转次数（1810 分）

题目

分析

#1

#2

解答