3383：施法所需最低符文数量（★★）

2024-12-09 约 713 字预计阅读 2 分钟次阅读

力扣第 3383 题

题目

Alice 刚刚从巫师学校毕业，并且希望施展一个魔法咒语来庆祝。魔法咒语包含某些需要集中魔力的焦点，其中一些焦点含有作为咒语能量源的魔法水晶。焦点可以通过 有向符文 进行连接，这些符文将魔力流从一个焦点传输到另一个焦点。

给定一个整数 n 表示焦点的数量，以及一个整数数组 crystals，其中 crystals[i] 表示有魔法水晶的焦点。同时给定两个整数数组 flowFrom 和 flowTo，表示存在的 有向符文。第 i^th 个符文允许魔力流从焦点 flowFrom[i] 传输到焦点 flowTo[i]。

你需要找到 Alice 必须添加到她的咒语中的定向符文数量，使得每个焦点要么：

包含一个魔法水晶。
从其它焦点接收魔力流。

返回她所需要添加的最少有向符文数量。

示例 1：

输入：n = 6, crystals = [0], flowFrom = [0,1,2,3], flowTo = [1,2,3,0]

输出：2

解释：

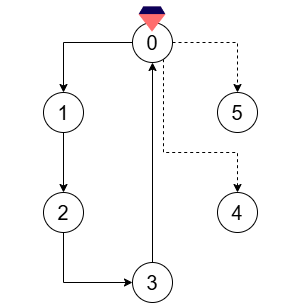
添加两个有向符文：

从焦点 0 到焦点 4。
从焦点 0 到焦点 5。

示例 2：

输入：n = 7, crystals = [3,5], flowFrom = [0,1,2,3,5], flowTo = [1,2,0,4,6]

输出：1

解释：

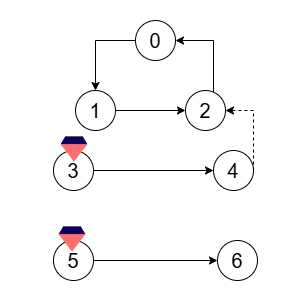
添加从焦点 4 到焦点 2 的有向符文。

提示：

2 <= n <= 10⁵
1 <= crystals.length <= n
0 <= crystals[i] <= n - 1
1 <= flowFrom.length == flowTo.length <= min(2 * 10⁵, (n * (n - 1)) / 2)
0 <= flowFrom[i], flowTo[i] <= n - 1
flowFrom[i] != flowTo[i]
所有的有向符文 互不相同。

相似问题：

分析

按强连通分量缩点后，统计没有符文的根即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


# 非递归 tarjan 求有向图强连通分量
def tarjan(g,n):
	def dfs(u):
		nonlocal i,j
		dq = [u]
		while dq:
			u = dq.pop()
			if p[u]==0:
				dfn[u] = low[u] = i = i+1
				sk.append(u)
			if p[u]<len(g[u]):
				dq.append(u)
				v = g[u][p[u]]
				if not dfn[v]:
					dq.append(v)
				p[u] += 1
			else:
				for v in g[u]:
					if not scc[v]:
						low[u] = min(low[u],low[v])
				if low[u]==dfn[u]:
					j += 1
					v = -1
					while v!=u:
						v = sk.pop()
						scc[v] = j

	dfn,low= [0]*n,[0]*n
	sk,p = [],[0]*n
	scc = [0]*n
	i,j = 0,0
	for u in range(n):
		if not dfn[u]:
			dfs(u)
	return scc

class Solution:
    def minRunesToAdd(self, n: int, crystals: List[int], flowFrom: List[int], flowTo: List[int]) -> int:
        g = [[] for _ in range(n)]
        for u,v in zip(flowFrom,flowTo):
            g[u].append(v)
        scc = tarjan(g,n)
        deg = [0]*(max(scc)+1)
        for u,v in zip(flowFrom,flowTo):
            if scc[u]!=scc[v]:
                deg[scc[v]] += 1
        for x in crystals:
            deg[scc[x]] += 1
        return sum(x==0 for x in deg[1:])

515 ms

目录

3383：施法所需最低符文数量（★★）

题目

分析

解答