力扣第 204 场周赛第 3 题
题目
给你一个大小为 m x n ,由若干 0 和 1 组成的二维网格 grid ,其中 1 表示陆地, 0 表示水。岛屿 由水平方向或竖直方向上相邻的 1 (陆地)连接形成。
如果 恰好只有一座岛屿 ,则认为陆地是 连通的 ;否则,陆地就是 分离的 。
一天内,可以将 任何单个 陆地单元(1)更改为水单元(0)。
返回使陆地分离的最少天数。
示例 1:
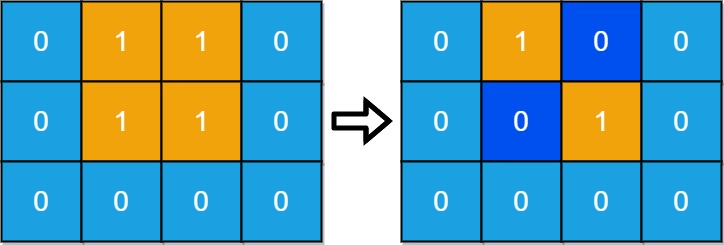
输入:grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]
输出:2
解释:至少需要 2 天才能得到分离的陆地。
将陆地 grid[1][1] 和 grid[0][2] 更改为水,得到两个分离的岛屿。
示例 2:

输入:grid = [[1,1]]
输出:2
解释:如果网格中都是水,也认为是分离的 ([[1,1]] -> [[0,0]]),0 岛屿。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j] 为 0 或 1
相似问题:
分析
#1
观察发现,只要岛屿有对角相连的网格,那么将该 2x2 的区域内的其它网格置 0,即可让岛屿分离。
因此最多需要两天。那么:
假如一开始就没有岛屿或者多个岛屿,返回 0
遍历岛屿网格,若置为 0 后岛屿分离,返回 1
其它情况,返回 2
计算岛屿数量,用并查集即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
def minDays(self, grid: List[List[int]]) -> int:
def find(x):
if f.setdefault(x,x) != x:
f[x] = find(f[x])
return f[x]
def union(x, y):
f[find(x)] = find(y)
def cal(A):
f.clear()
for i, j in A:
for x, y in [(i-1, j), (i, j-1), (i+1, j), (i, j+1)]:
if (x, y) in A:
union((i, j), (x, y))
return len({find((i, j)) for i,j in A})
m, n = len(grid), len(grid[0])
f, A = {}, {(i, j) for i in range(m) for j in range(n) if grid[i][j]}
if cal(A) != 1:
return 0
return 1 if any(cal(A-{a})!=1 for a in A) else 2
|
时间复杂度 O(m^2*n^2),7496 ms
#2
找某个岛屿网格,使得去掉后岛屿分离,这其实就是找无向图的割点,可以用 tarjan 算法。
注意特殊情况,岛屿只有一个网格时,没有割点,但只需要 1 天
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
def minDays(self, grid: List[List[int]]) -> int:
def find(x):
if f.setdefault(x,x) != x:
f[x] = find(f[x])
return f[x]
def union(x, y):
f[find(x)] = find(y)
def cal(A):
f.clear()
for i, j in A:
for x, y in [(i-1, j), (i, j-1), (i+1, j), (i, j+1)]:
if (x, y) in A:
union((i, j), (x, y))
return len({find((i, j)) for i,j in A})
def tarjan(p, isroot):
self.idx += 1
dfn[p] = low[p] = self.idx
tot, (i, j) = 0, p
for q in [(i-1, j), (i, j-1), (i+1, j), (i, j+1)]:
if q in A:
if q not in dfn:
tarjan(q, False)
low[p] = min(low[p], low[q])
tot += low[q] >= dfn[p]
else:
low[p] = min(low[p], dfn[q])
if tot>int(isroot):
cut.append(p)
m, n = len(grid), len(grid[0])
f, A = {}, {(i, j) for i in range(m) for j in range(n) if grid[i][j]}
if len(A) == 1:
return 1
if cal(A) != 1:
return 0
cut, dfn, low, self.idx = [], {}, {}, 0
tarjan(next(iter(A)), True)
return 1 if cut else 2
|
时间复杂度 O(m*n),108 ms

