3359：查找最大元素不超过 K 的有序子矩阵（★★）

Ian

2024-11-20 约 431 字预计阅读 1 分钟次阅读

力扣第 3359 题

题目

给定一个大小为 m x n 的二维矩阵 grid。同时给定一个 非负整数 k。

返回满足下列条件的 grid 的子矩阵数量：

子矩阵中最大的元素 小于等于 k。
子矩阵的每一行都以 非递增 顺序排序。

矩阵的子矩阵 (x1, y1, x2, y2) 是通过选择所有满足 x1 <= x <= x2 且 y1 <= y <= y2 的 grid[x][y] 元素组成的矩阵。

示例 1：

输入：grid = [[4,3,2,1],[8,7,6,1]], k = 3

输出：8

解释：

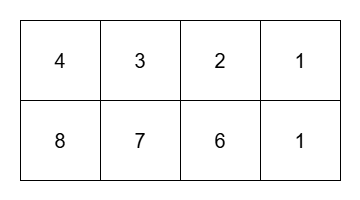
8 个子矩阵分别是：

[[1]]
[[1]]
[[2,1]]
[[3,2,1]]
[[1],[1]]
[[2]]
[[3]]
[[3,2]]

示例 2：

输入：grid = [[1,1,1],[1,1,1],[1,1,1]], k = 1

输出：36

解释：

矩阵中有 36 个子矩阵。所有子矩阵的最大元素都等于 1。

示例 3：

输入：grid = [[1]], k = 1

输出：1

提示：

1 <= m == grid.length <= 10³
1 <= n == grid[i].length <= 10³
1 <= grid[i][j] <= 10⁹
1 <= k <= 10⁹

相似问题：

0085：最大矩形

分析

类似 1504，枚举每一列作为右边界，转为柱形图，单调栈+dp 解决

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution:
    def countSubmatrices(self, grid: List[List[int]], k: int) -> int:
        def cal(A):
            res = 0
            f = [0]*len(A)
            sk = []
            for j,a in enumerate(A):
                while sk and A[sk[-1]]>=a:
                    sk.pop()
                i = sk[-1] if sk else -1
                f[j] = f[i]+(j-i)*a
                res += f[j]
                sk.append(j)
            return res

        m,n = len(grid),len(grid[0])
        f = [0]*m
        res = 0
        for j in range(n):
            for i in range(m):
                if grid[i][j]>k:
                    f[i] = 0
                else:
                    f[i] = 1+(f[i] if j==0 or grid[i][j]<=grid[i][j-1] else 0)
            res += cal(f)
        return res

854 ms

目录

3359：查找最大元素不超过 K 的有序子矩阵（★★）

题目

分析

解答