1504：统计全 1 子矩形（1845 分）

力扣第 196 场周赛第 3 题

题目

给你一个 m x n 的二进制矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

示例 1：

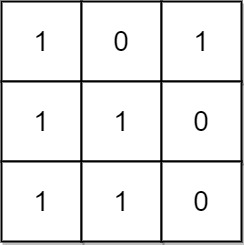
输入：mat = [[1,0,1],[1,1,0],[1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

示例 2：

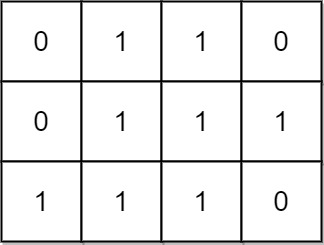
输入：mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。

提示：

• 1 <= m, n <= 150
• mat[i][j] 仅包含 0 或 1

相似问题：

• 3212：统计 X 和 Y 频数相等的子矩阵数量（1672 分）

分析

• 类似 0085，可以遍历每一行作为底，转为柱形图，用单调栈求解
• 假设柱子 j 上一个更小的柱子为 i，那么以 j 为右边界的矩形
  • 要么左边界<=i，即对应了以 i 为右边界的矩形
  • 要么左边界在 i 和 j 之间，高度都可以取到柱子 j 的高度
• 因此维护单调栈的同时用 dp 递推即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        res, H = 0, [0]*n
        for i in range(m):
            H = [a+1 if b else 0 for a,b in zip(H,mat[i])]
            sk = []
            f = [0]*n
            for j,x in enumerate(H):
                while sk and H[sk[-1]]>=x:
                    sk.pop()
                i = sk[-1] if sk else -1
                f[j] = f[i]+(j-i)*x
                res += f[j]
                sk.append(j)
        return res

35 ms