3027：人员站位的方案数 II（2020 分）

2024-02-03 约 1571 字预计阅读 4 分钟次阅读

力扣第 123 场双周赛第 4 题

题目

给你一个 n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [x_i, y_i] 。

我们定义 x 轴的正方向为右（x 轴递增的方向），x 轴的负方向为左（x 轴递减的方向）。类似的，我们定义 y 轴的正方向为上（y 轴递增的方向），y 轴的负方向为下（y 轴递减的方向）。

你需要安排这 n 个人的站位，这 n 个人中包括 Alice 和 Bob 。你需要确保每个点处恰好有一个人。同时，Alice 想跟 Bob 单独玩耍，所以 Alice 会以 Alice 的坐标为 左上角 ，Bob 的坐标为 右下角 建立一个矩形的围栏（注意，围栏可能不包含任何区域，也就是说围栏可能是一条线段）。如果围栏的内部或者边缘上有任何其他人，Alice 都会难过。

请你在确保 Alice 不会难过的前提下，返回 Alice 和 Bob 可以选择的点对数目。

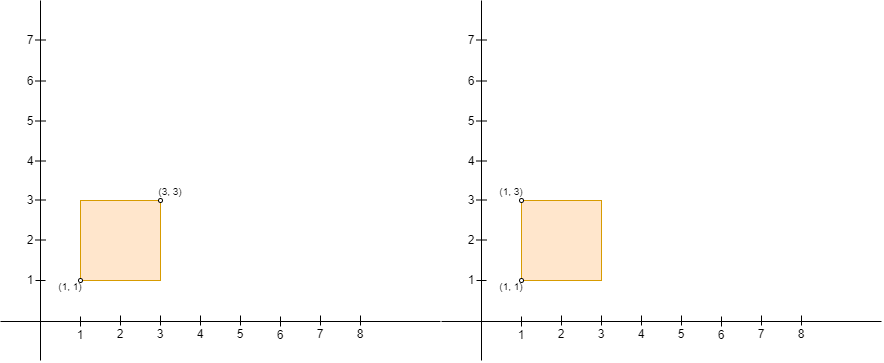
注意，Alice 建立的围栏必须确保 Alice 的位置是矩形的左上角，Bob 的位置是矩形的右下角。比方说，以 (1, 1) ，(1, 3) ，(3, 1) 和 (3, 3) 为矩形的四个角，给定下图的两个输入，Alice 都不能建立围栏，原因如下：

图一中，Alice 在 (3, 3) 且 Bob 在 (1, 1) ，Alice 的位置不是左上角且 Bob 的位置不是右下角。
图二中，Alice 在 (1, 3) 且 Bob 在 (1, 1)（如图所示，用矩形代替线条），Bob 的位置不是在围栏的右下角。

示例 1：

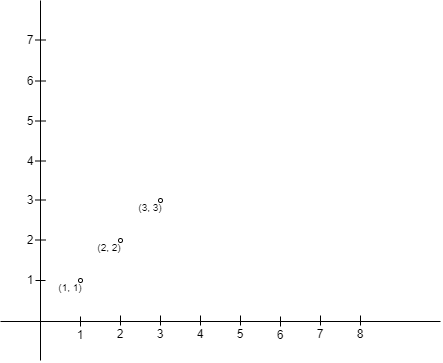
输入：points = [[1,1],[2,2],[3,3]]
输出：0
解释：没有办法可以让 Alice 的围栏以 Alice 的位置为左上角且 Bob 的位置为右下角。所以我们返回 0 。

示例 2：

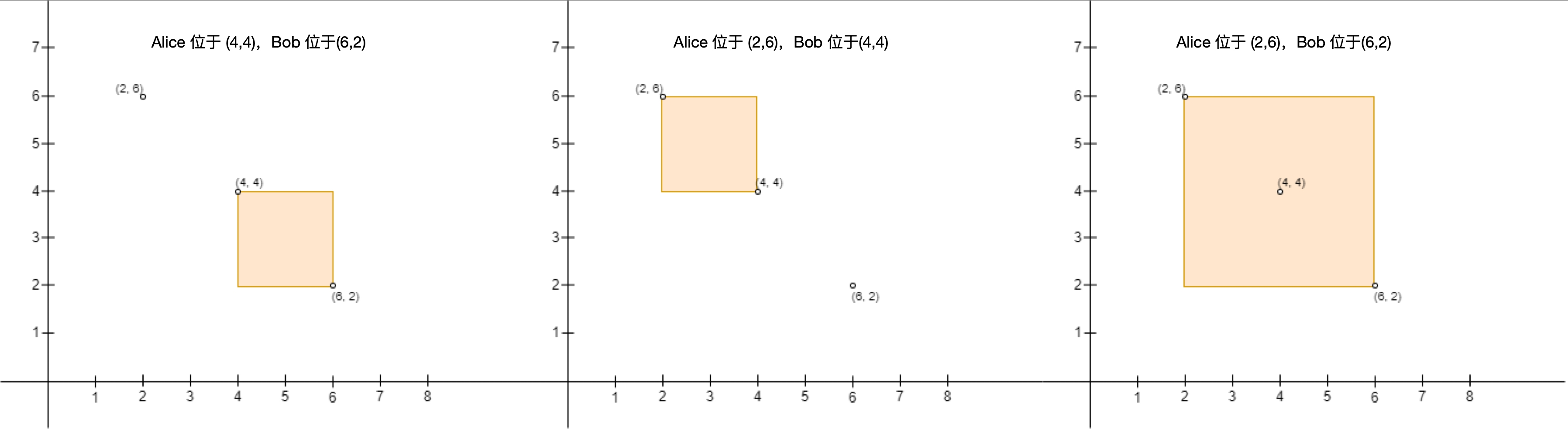
输入：points = [[6,2],[4,4],[2,6]]
输出：2
解释：总共有 2 种方案安排 Alice 和 Bob 的位置，使得 Alice 不会难过：
- Alice 站在 (4, 4) ，Bob 站在 (6, 2) 。
- Alice 站在 (2, 6) ，Bob 站在 (4, 4) 。
不能安排 Alice 站在 (2, 6) 且 Bob 站在 (6, 2) ，因为站在 (4, 4) 的人处于围栏内。

示例 3：

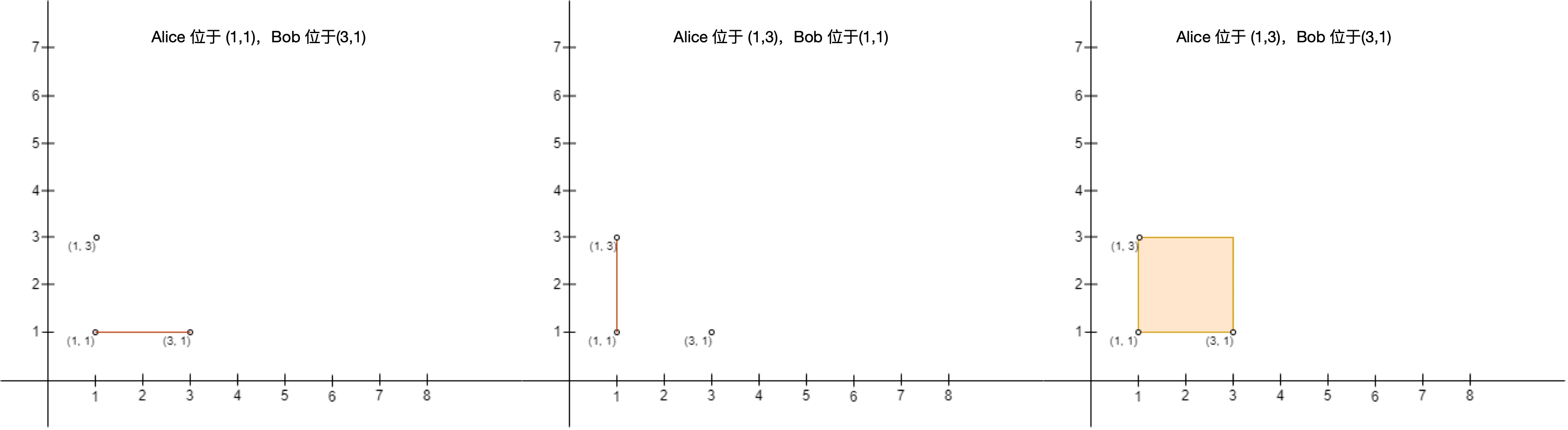
输入：points = [[3,1],[1,3],[1,1]]
输出：2
解释：总共有 2 种方案安排 Alice 和 Bob 的位置，使得 Alice 不会难过：
- Alice 站在 (1, 1) ，Bob 站在 (3, 1) 。
- Alice 站在 (1, 3) ，Bob 站在 (1, 1) 。
不能安排 Alice 站在 (1, 3) 且 Bob 站在 (3, 1) ，因为站在 (1, 1) 的人处于围栏内。
注意围栏是可以不包含任何面积的，上图中第一和第二个围栏都是合法的。

提示：

2 <= n <= 1000
points[i].length == 2
-10⁹ <= points[i][0], points[i][1] <= 10⁹
points[i] 点对两两不同。

相似问题：

0223：矩形面积

分析

#1

先不考虑 x 相等的点，将坐标排序得到 A
- 即是要找点对 (i,j),i<j，满足 A[i].y>=A[j].y，且 all(A[k].y>A[i].y or A[k].y<A[j].y for k in range(i,j))
- 固定 i，遍历 j，即是要满足 max(A[k].y for k in range(i,j) if A[k].y<=A[i].y)<A[j].y
- 维护这个 max 值即可
对于 x 相等的点，要找 y1>y2 且 y1和y2间没有其它点，因此按 y 降序排序即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        points.sort(key=lambda p: (p[0],-p[1]))
        A = [y for _,y in points]
        n = len(A)
        res = 0
        for i in range(n):
            ma = -inf
            for j in range(i+1,n):
                if ma<A[j]<=A[i]:
                    res += 1
                    ma = A[j]
        return res

1334 ms

#2

可以用 cdq 分治优化

类似的，先按 (x升序,y降序) 得到排序后的 y 坐标数组 h
对于区间 (l,r)，要计算左半 (l,m) 和右半 (m+1,r) 之间的点对个数
先不考虑相等的情况，从小到大遍历区间 (l,r) 的元素 A
- 对于下标 i 的元素 a
- 假如 i>m，a 属于右半部分，将 i 添加到数组 C 中
  - 注意到假如 j=C[-1]>i，由于下标 j 的元素 b<a，对于之后的左半部分的点而言，下标 j 都不可能配对
  - 因此右半部分可以维护一个单调栈 sk2 保存有效的点
- 假如 i<=m，a 属于左半部分，将 i 添加到数组 B 中
  - 计算右半部分有多少个点能和 a 配对
  - 首先，要考虑区间 (i+1,m) 已遍历的元素最大值 b
    - 即是找 B 中上一个大于 i 的元素，可以用单调栈 sk1 维护
  - 然后，对于右半部分的单调栈 sk2，只要元素值大于 b 即有效，二分即可
接着考虑相等的情况
- 对于左半部分，要令区间 (i+1,m) 已遍历的元素最大值等价于实际的限制值，较大的下标就必须先遍历
- 对于右半部分，要令单调栈严格递增，较大的下标也必须先遍历
- 因此，按照 (元素升序,下标降序) 遍历
再递归计算 (B,l,m),(C,m+1,r) 即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        def cdq(A,l,r):
            if l==r:
                return 0
            m = (l+r)//2
            res = 0
            B,C = [],[]
            sk1,sk2 = [],[]
            for i in A:
                if i<=m:
                    B.append(i)
                    while sk1 and sk1[-1]<i:
                        sk1.pop()
                    res += len(sk2)
                    if sk1:
                        y = h[sk1[-1]]
                        res -= bisect_right(sk2,y,key=lambda j:h[j])
                    sk1.append(i)
                else:
                    C.append(i)
                    while sk2 and sk2[-1]>i:
                        sk2.pop()
                    sk2.append(i)
            return res+cdq(B,l,m)+cdq(C,m+1,r)

        points.sort(key=lambda p:(p[0],-p[1]))
        h = [y for _,y in points]
        n = len(h)
        A = sorted(range(n),key=lambda i:[h[i],-i])
        return cdq(A,0,n-1)

520 ms

目录

3027：人员站位的方案数 II（2020 分）

题目

分析

#1

#2