2371：最小化网格中的最大值（★★）

力扣第 2371 题

题目

给定一个包含 不同 正整数的 m × n 整数矩阵 grid。

必须将矩阵中的每一个整数替换为正整数，且满足以下条件:

• 在替换之后，同行或同列中的每两个元素的 相对 顺序应该保持 不变。
• 替换后矩阵中的 最大 数目应尽可能 小。

如果对于原始矩阵中的所有元素对，使 grid[r1][c1] > grid[r2][c2]，其中要么 r1 == r2 ，要么 c1 == c2，则相对顺序保持不变。那么在替换之后一定满足 grid[r1][c1] > grid[r2][c2]。

例如，如果 grid = [[2, 4, 5], [7, 3, 9]]，那么一个好的替换可以是 grid = [[1, 2, 3], [2, 1, 4]] 或 grid = [[1, 2, 3], [3, 1, 4]]。

返回 结果 矩阵。如果有多个答案，则返回其中 任何 一个。

示例 1:

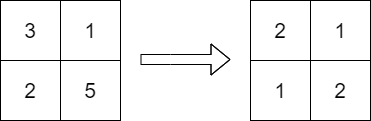
输入: grid = [[3,1],[2,5]]
输出: [[2,1],[1,2]]
解释: 上面的图显示了一个有效的替换。
矩阵中的最大值是 2。可以证明，不能得到更小的值。

示例 2:

输入: grid = [[10]]
输出: [[1]]
解释: 我们将矩阵中唯一的数字替换为 1。

提示:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• 1 <= grid[i][j] <= 109
• grid 由不同的整数组成。

相似问题：

• 0135：分发糖果

分析

• 从小到大遍历格子，并维护每行/列的最大值
• 格子的值只要比该行/列的最大值大即可

解答

1
2
3
4
5
6
7
8
9

class Solution:
    def minScore(self, grid: List[List[int]]) -> List[List[int]]:
        m,n = len(grid),len(grid[0])
        R = [0]*m
        C = [0]*n
        res = [[0]*n for _ in range(m)]
        for x,i,j in sorted([grid[i][j],i,j] for i in range(m) for j in range(n)):
            R[i] = C[j] = res[i][j] = max(R[i],C[j])+1
        return res

413 ms