0973：最接近原点的 K 个点（1213 分）

力扣第 119 场周赛第 1 题

题目

给定一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点，并且是一个整数 k ，返回离原点 (0,0) 最近的 k 个点。

这里，平面上两点之间的距离是 欧几里德距离（ √(x1 - x2)2 + (y1 - y2)2 ）。

你可以按 任何顺序 返回答案。除了点坐标的顺序之外，答案 确保 是 唯一 的。

示例 1：

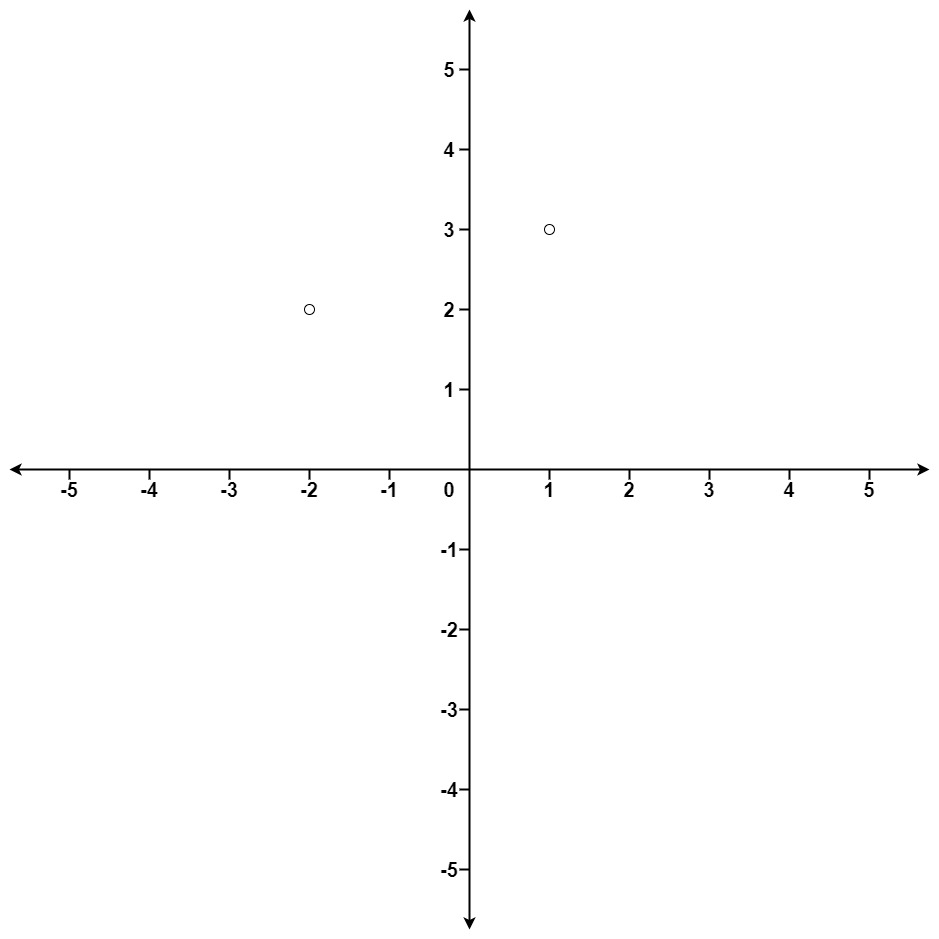
输入：points = [[1,3],[-2,2]], k = 1
输出：[[-2,2]]
解释： 
(1, 3) 和原点之间的距离为 sqrt(10)，
(-2, 2) 和原点之间的距离为 sqrt(8)，
由于 sqrt(8) < sqrt(10)，(-2, 2) 离原点更近。
我们只需要距离原点最近的 K = 1 个点，所以答案就是 [[-2,2]]。

示例 2：

输入：points = [[3,3],[5,-1],[-2,4]], k = 2
输出：[[3,3],[-2,4]]
（答案 [[-2,4],[3,3]] 也会被接受。）

提示：

• 1 <= k <= points.length <= 104
• -104 < xi, yi < 104

相似问题：

• 0215：数组中的第K个最大元素
• 0347：前 K 个高频元素
• 0692：前K个高频单词
• 1779：找到最近的有相同 X 或 Y 坐标的点（1259 分）
• 3111：覆盖所有点的最少矩形数目（1401 分）

分析

按距离排序或者用 heapq.nsmallest 即可。

解答

1
2

def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
	return nsmallest(k, points, key=lambda x: x[0]*x[0]+x[1]*x[1])

172 ms