0335：路径交叉（★★）

2015-12-01 约 423 字预计阅读 1 分钟次阅读

力扣第 335 题

题目

给你一个整数数组 distance 。

从 X-Y 平面上的点 (0,0) 开始，先向北移动 distance[0] 米，然后向西移动 distance[1] 米，向南移动 distance[2] 米，向东移动 distance[3] 米，持续移动。也就是说，每次移动后你的方位会发生逆时针变化。

判断你所经过的路径是否相交。如果相交，返回 true ；否则，返回 false 。

示例 1：

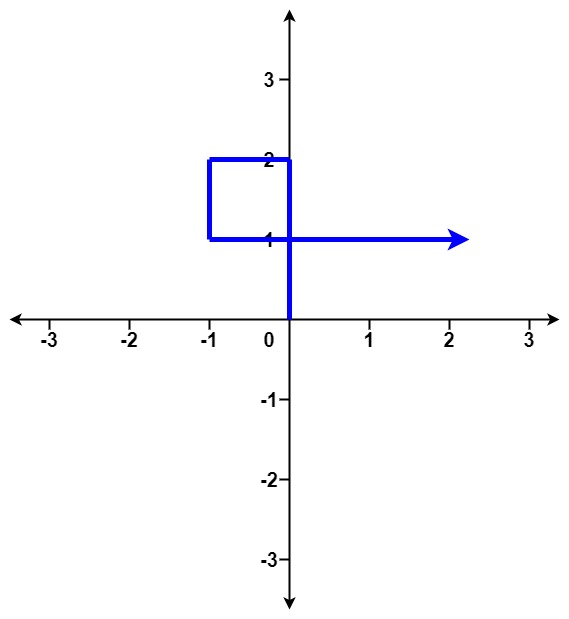
输入：distance = [2,1,1,2]
输出：true

示例 2：

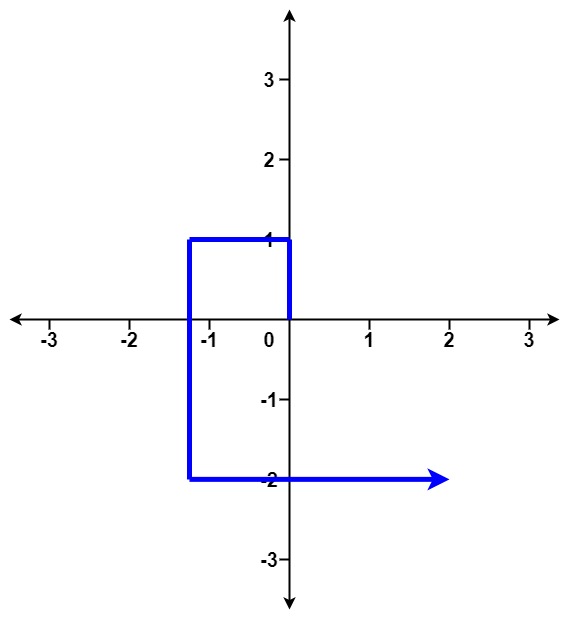
输入：distance = [1,2,3,4]
输出：false

示例 3：

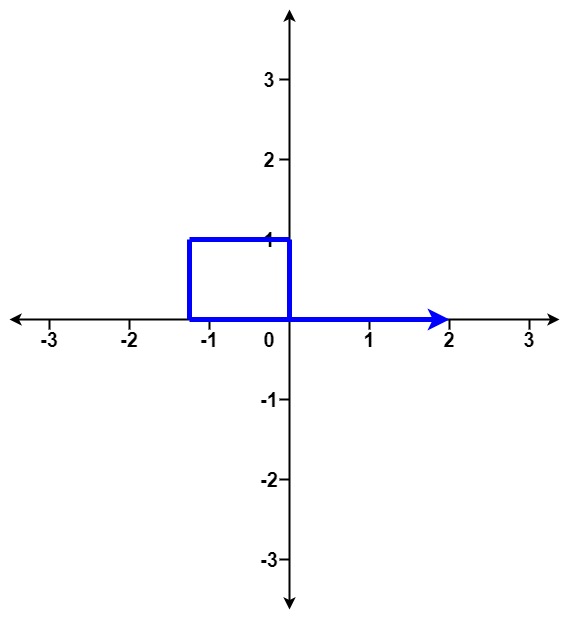
输入：distance = [1,1,1,1]
输出：true

提示：

1 <= distance.length <= 10⁵
1 <= distance[i] <= 10⁵

分析

#1

观察发现，第 i 步的路径只可能和 i+3、i+4、i+5 的路径交叉
判断路径交叉可以用类似 0223 的方法，看 x/y 方向上是否重叠
遍历时保存每个端点，分别判断即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


class Solution:
    def isSelfCrossing(self, distance: List[int]) -> bool:
        def check(a1,a2,b1,b2):
            a1,a2 = sorted([a1,a2])
            b1,b2 = sorted([b1,b2])
            return all(max(a1[i],b1[i])<=min(a2[i],b2[i]) for i in range(2))

        A,dx,dy = [(0,0)],0,1
        for a in distance:
            A.append((A[-1][0]+dx*a,A[-1][1]+dy*a))
            dx,dy = -dy,dx
            for i in range(4,min(7,len(A))):
                if check(A[-1],A[-2],A[-i],A[-i-1]):
                    return True
        return False

491 ms

#2

还可以继续观察，直接找交叉时距离之间的规律，具体见力扣官解。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


class Solution:
    def isSelfCrossing(self, distance: List[int]) -> bool:
        A = distance
        for i in range(3,len(A)):
            if A[i]>=A[i-2] and A[i-1]<=A[i-3]:
                return True
            if i>=4 and A[i-1]==A[i-3] and A[i]+A[i-4]>=A[i-2]:
                return True
            if i>=5 and A[i]+A[i-4]>=A[i-2]>=A[i-4] and A[i-1]+A[i-5]>=A[i-3]>=A[i-1]:
                return True
        return False

64 ms

目录

0335：路径交叉（★★）

题目

分析

#1

#2

解答