0319：灯泡开关（★）

力扣第 319 题

题目

初始时有 n 个灯泡处于关闭状态。第一轮，你将会打开所有灯泡。接下来的第二轮，你将会每两个灯泡关闭第二个。

第三轮，你每三个灯泡就切换第三个灯泡的开关（即，打开变关闭，关闭变打开）。第 i 轮，你每 i 个灯泡就切换第 i 个灯泡的开关。直到第 n 轮，你只需要切换最后一个灯泡的开关。

找出并返回 n 轮后有多少个亮着的灯泡。

示例 1：

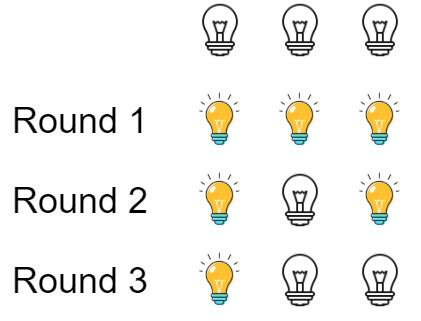
输入：n = 3
输出：1
解释：
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭].

你应该返回 1，因为只有一个灯泡还亮着。

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：1

提示：

• 0 <= n <= 109

相似问题：

• 0672：灯泡开关 Ⅱ
• 0995：K 连续位的最小翻转次数（1835 分）
• 1375：二进制字符串前缀一致的次数（1438 分）
• 2485：找出中枢整数（1207 分）

分析

可以观察每个位置的灯泡切换了多少次：

• 位置 x 的灯泡，第 i 轮切换等价于 x % i == 0
• 位置 x 的灯泡的切换次数即为 x 的因数个数
• 根据数学知识，只有完全平方数有奇数个因数，其它都是偶数个因数
• 因此计算 1 到 n 有多少个完全平方数即可

解答

1
2
3

class Solution:
    def bulbSwitch(self, n: int) -> int:
        return isqrt(n)

32 ms