0308:二维区域和检索 - 可变(★★)
目录
题目
给你一个二维矩阵 matrix ,处理以下类型的多个查询:
- 更新
matrix中单元格的值。 - 计算由 左上角
(row1, col1)和 右下角(row2, col2)定义的matrix内矩阵元素的 和。
实现 NumMatrix 类:
NumMatrix(int[][] matrix)用整数矩阵matrix初始化对象。void update(int row, int col, int val)更新matrix[row][col]的值到val。int sumRegion(int row1, int col1, int row2, int col2)返回矩阵matrix中指定矩形区域元素的 和 ,该区域由 左上角(row1, col1)和 右下角(row2, col2)界定。
示例 1:
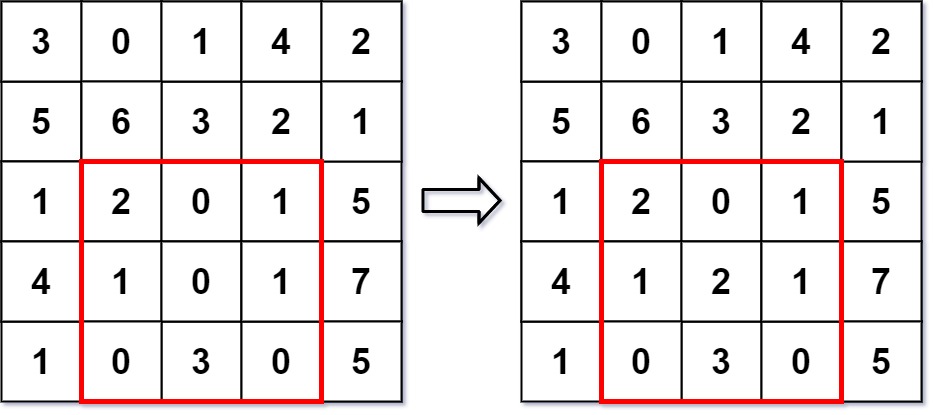
输入 ["NumMatrix", "sumRegion", "update", "sumRegion"] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [3, 2, 2], [2, 1, 4, 3]] 输出 [null, 8, null, 10]解释 NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]); numMatrix.sumRegion(2, 1, 4, 3); // 返回 8 (即, 左侧红色矩形的和) numMatrix.update(3, 2, 2); // 矩阵从左图变为右图 numMatrix.sumRegion(2, 1, 4, 3); // 返回 10 (即,右侧红色矩形的和)
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200-105 <= matrix[i][j] <= 1050 <= row < m0 <= col < n-105 <= val <= 1050 <= row1 <= row2 < m0 <= col1 <= col2 < n- 最多调用
104次sumRegion和update方法
分析
0304 升级版,元素不固定了。
朴素的想法是维护每一行的前缀和即可,update 时间 O(N),sumRegion 时间 O(M)。
解答
|
|
52 ms
*附加
类似 0307 ,也可以用树状数组解决,采用二维树状数组。
|
|
320 ms