3313：查找树中最后标记的节点（★★）

2024-10-12 约 1067 字预计阅读 3 分钟次阅读

力扣第 3313 题

题目

有一棵有 n 个节点，编号从 0 到 n - 1 的无向树。给定一个长度为 n - 1 的整数数组 edges，其中 edges[i] = [u_i, v_i] 表示树中的 u_i 和 v_i 之间有一条边。

一开始，所有节点都 未标记。之后的每一秒，你需要标记所有至少有一个已标记节点相邻的未标记节点。

返回一个数组 nodes，表示在时刻 t = 0 标记了节点 i，那么树中最后标记的节点是 nodes[i]。如果对于任意节点 i 有多个 nodes[i]，你可以选择任意一个作为答案。

示例 1：

输入：edges = [[0,1],[0,2]]

输出：[2,2,1]

解释：

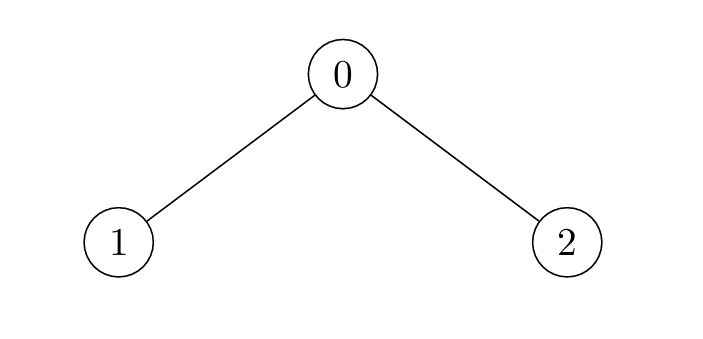
对于 i = 0，节点以如下序列标记：[0] -> [0,1,2]。1 和 2 都可以是答案。
对于 i = 1，节点以如下序列标记：[1] -> [0,1] -> [0,1,2]。节点 2 最后被标记。
对于 i = 2，节点以如下序列标记：[2] -> [0,2] -> [0,1,2]。节点 1 最后被标记。

示例 2：

输入：edges = [[0,1]]

输出：[1,0]

解释：

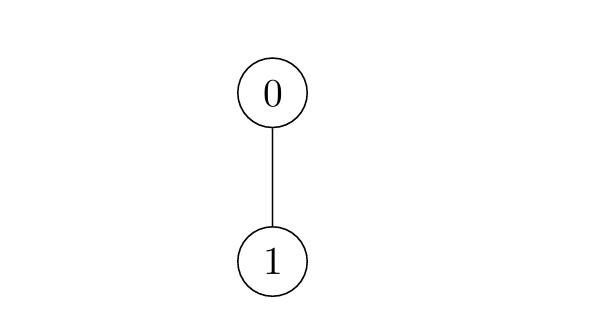
对于 i = 0，节点以如下序列被标记：[0] -> [0,1]。
对于 i = 1，节点以如下序列被标记：[1] -> [0,1]。

示例 3：

输入：edges = [[0,1],[0,2],[2,3],[2,4]]

输出：[3,3,1,1,1]

解释：

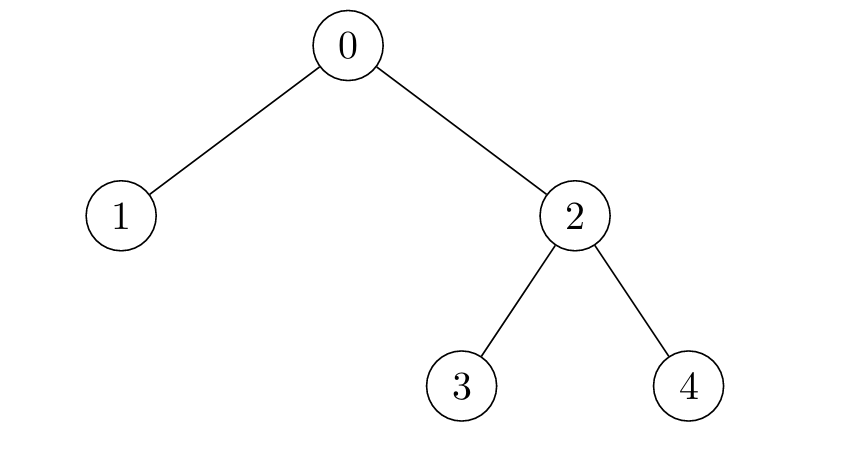
对于 i = 0，节点以如下序列被标记：[0] -> [0,1,2] -> [0,1,2,3,4]。
对于 i = 1，节点以如下序列被标记：[1] -> [0,1] -> [0,1,2] -> [0,1,2,3,4]。
对于 i = 2，节点以如下序列被标记：[2] -> [0,2,3,4] -> [0,1,2,3,4]。
对于 i = 3，节点以如下序列被标记：[3] -> [2,3] -> [0,2,3,4] -> [0,1,2,3,4]。
对于 i = 4，节点以如下序列被标记：[4] -> [2,4] -> [0,2,3,4] -> [0,1,2,3,4]。

提示：

2 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= edges[i][0], edges[i][1] <= n - 1
输入保证 edges 形成一棵合法的树。

相似问题：

分析

#1

典型的换根dp，同时保存最远的节点即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


# dfs序预处理树
def prep(edges):
    n = len(edges)+1
    g = [[] for _ in range(n)]
    for u,v in edges:
        g[u].append(v)
        g[v].append(u)
    fa = [-1]*n
    order = []
    sk = [0]
    while sk:
        u = sk.pop()
        order.append(u)
        g[u] = [v for v in g[u] if v!=fa[u]]
        for v in g[u]:
            fa[v] = u
            sk.append(v)
    return g,order,fa

class Solution:
    def lastMarkedNodes(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)+1
        g,order,fa = prep(edges)
        f = [[0,u] for u in range(n)]
        for u in order[::-1]:
            for v in g[u]:
                a,b = f[v]
                f[u] = max(f[u],[1+a,b])
        up = [[] for _ in range(n)]
        for u in order:
            m1,m2 = nlargest(2,[[f[v][0]+1,f[v][1]] for v in g[u]]+[up[u],[0,0]])
            for v in g[u]:
                x = m2 if [f[v][0]+1,f[v][1]]==m1 else m1
                up[v] = [x[0]+1,x[1]]
                f[v] = max(f[v],up[v])
        return [p[1] for p in f]

2082 ms

#2

也可以先两次 bfs 找到直径的两个端点 u、v
树上任意节点距离最远的必然是 u、v 其中之一，比较即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


class Solution:
    def lastMarkedNodes(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)+1
        g = [[] for _ in range(n)]
        for u,v in edges:
            g[u].append(v)
            g[v].append(u)
        def bfs(u):
            d = [-1]*n
            d[u] = 0
            dq = deque([u])
            while dq:
                u = dq.popleft()
                for v in g[u]:
                    if d[v]==-1:
                        d[v] = d[u]+1
                        dq.append(v)
            return d
        d = bfs(0)
        u = d.index(max(d))
        d2 = bfs(u)
        v = d2.index(max(d2))
        d3 = bfs(v)
        return [max((d2[x],u),(d3[x],v))[1] for x in range(n)]

522 ms

目录

3313：查找树中最后标记的节点（★★）

题目

分析

#1

#2

解答