力扣第 135 场双周赛第 4 题
题目
给你一个大小为 n x n 的二维矩阵 grid ,一开始所有格子都是白色的。一次操作中,你可以选择任意下标为 (i, j) 的格子,并将第 j 列中从最上面到第 i 行所有格子改成黑色。
如果格子 (i, j) 为白色,且左边或者右边的格子至少一个格子为黑色,那么我们将 grid[i][j] 加到最后网格图的总分中去。
请你返回执行任意次操作以后,最终网格图的 最大 总分数。
示例 1:
输入:grid = [[0,0,0,0,0],[0,0,3,0,0],[0,1,0,0,0],[5,0,0,3,0],[0,0,0,0,2]]
输出:11
解释:
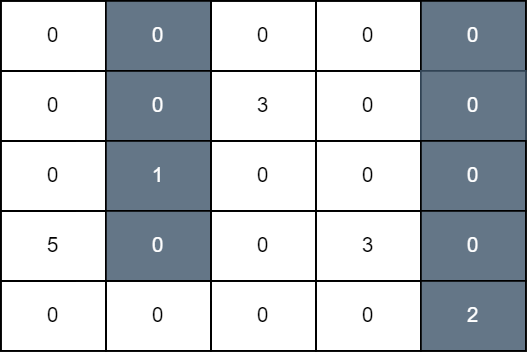
第一次操作中,我们将第 1 列中,最上面的格子到第 3 行的格子染成黑色。第二次操作中,我们将第 4 列中,最上面的格子到最后一行的格子染成黑色。最后网格图总分为 grid[3][0] + grid[1][2] + grid[3][3] 等于 11 。
示例 2:
输入:grid = [[10,9,0,0,15],[7,1,0,8,0],[5,20,0,11,0],[0,0,0,1,2],[8,12,1,10,3]]
输出:94
解释:
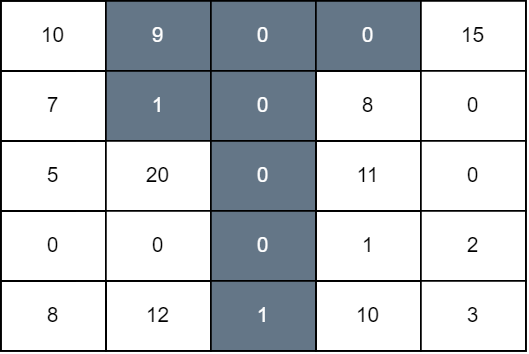
我们对第 1 ,2 ,3 列分别从上往下染黑色到第 1 ,4, 0 行。最后网格图总分为 grid[0][0] + grid[1][0] + grid[2][1] + grid[4][1] + grid[1][3] + grid[2][3] + grid[3][3] + grid[4][3] + grid[0][4] 等于 94 。
提示:
1 <= n == grid.length <= 100n == grid[i].length0 <= grid[i][j] <= 109
相似问题:
分析
#1
- 先考虑朴素递推,令 f [i] 代表遍历到第 x 列且该列染 i 行时的最大得分
- 遍历第 x-1 列染 j 行
- 若 j>=i,相对于 f[x-1][j] 只多了 x 列 [i,j] 的分数和
- 若 j<i,则要考虑 x-1 列哪些分数已经被计算
- 遍历第 x-2 列染 k 行
- 若 k<=j,则 x-1 列分数都未计算,相对于 f[x-1][j] 多了 x-1 列 [j,i] 的分数和
- 若 k>j,相对于 f[x-2][k] 多了 x-1 列 [j,max(k,i)] 的分数和
- 为了区分 k<=j 和 k>j 两种情况下的 f[x-1][j] ,可以新加一个变量
- 令 f [i][0] 代表到第 x 列,染 i 行,且第 x-1 列的行数 j>=i 的最大得分
- 令 f [i][1] 代表到第 x 列,染 i 行,且第 x-1 列的行数 j<i 的最大得分
- 最后 f[-1] 中的最大值即为所求
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution:
def maximumScore(self, grid: List[List[int]]) -> int:
m,n = len(grid),len(grid[0])
C = [[0]+list(accumulate(col)) for col in zip(*grid)]
f = [[[0,0] for _ in range(n+1)] for _ in range(m)]
for x in range(1,m):
for i in range(n+1):
for j in range(i,n+1):
s = max(f[x-1][j])+C[x][j]-C[x][i]
f[x][i][0] = max(f[x][i][0],s)
for j in range(i):
s = f[x-1][j][1]+C[x-1][i]-C[x-1][j]
f[x][i][1] = max(f[x][i][1],s)
if x>1:
for j in range(i):
for k in range(j,n+1):
s = max(f[x-2][k])+C[x-1][max(k,i)]-C[x-1][j]
f[x][i][1] = max(f[x][i][1],s)
return max(max(p) for p in f[-1])
|
超时
#2
- 瓶颈在于 j<i 且 j<k 时的遍历
- 观察发现,此时 j 越小,分数越大,因此可以只考虑 j 为 0 的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def maximumScore(self, grid: List[List[int]]) -> int:
m,n = len(grid),len(grid[0])
C = [[0]+list(accumulate(col)) for col in zip(*grid)]
f = [[[0,0] for _ in range(n+1)] for _ in range(m)]
for x in range(1,m):
for i in range(n+1):
for j in range(i,n+1):
s = max(f[x-1][j])+C[x][j]-C[x][i]
f[x][i][0] = max(f[x][i][0],s)
for j in range(i):
s = f[x-1][j][1]+C[x-1][i]-C[x-1][j]
f[x][i][1] = max(f[x][i][1],s)
if x>1:
for k in range(n+1):
s = max(f[x-2][k])+C[x-1][max(k,i)]-C[x-1][0]
f[x][i][1] = max(f[x][i][1],s)
return max(max(p) for p in f[-1])
|
8249 ms
#3
- 观察 f [i][0] 的递推式,C [i] 是固定的,max(f[x-1][j])+C [j] for j in range(i,n+1) 是一个后缀最值
- 因此预先处理 max(f[x-1][j])+C [j] 的后缀最值,即可省去一重循环
- 同理,对 f [i][1] 的几个递推式也预处理前缀/后缀最值
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution:
def maximumScore(self, grid: List[List[int]]) -> int:
m,n = len(grid),len(grid[0])
C = [[0]+list(accumulate(col)) for col in zip(*grid)]
f = [[[0,0] for _ in range(n+1)] for _ in range(m)]
for x in range(1,m):
suf,pre = [0]*(n+2),[0]*(n+2)
for j in range(n,-1,-1):
suf[j] = max(suf[j+1],max(f[x-1][j])+C[x][j])
for j in range(n+1):
pre[j] = max(pre[j-1],f[x-1][j][1]-C[x-1][j])
for i in range(n+1):
f[x][i][0] = suf[i]-C[x][i]
f[x][i][1] = pre[i]+C[x-1][i]
if x>1:
suf,pre = [0]*(n+2),[0]*(n+2)
for k in range(n,-1,-1):
suf[k] = max(suf[k+1],max(f[x-2][k])+C[x-1][k])
for k in range(n+1):
pre[k] = max(pre[k-1],max(f[x-2][k]))
for i in range(n+1):
f[x][i][1] = max(f[x][i][1],suf[i]-C[x-1][0],pre[i]+C[x-1][i]-C[x-1][0])
return max(max(p) for p in f[-1])
|
306 ms

