3009：折线图上的最大交点数量（★★）

力扣第 3009 题

题目

有一条由 n 个点连接而成的折线图。给定一个 下标从 1 开始 的整数数组 y，第 k 个点的坐标是 (k, y[k])。图中没有水平线，即没有两个相邻的点有相同的 y 坐标。

假设在图中任意画一条无限长的水平线。请返回这条水平线与折线相交的最多交点数。

示例 1：

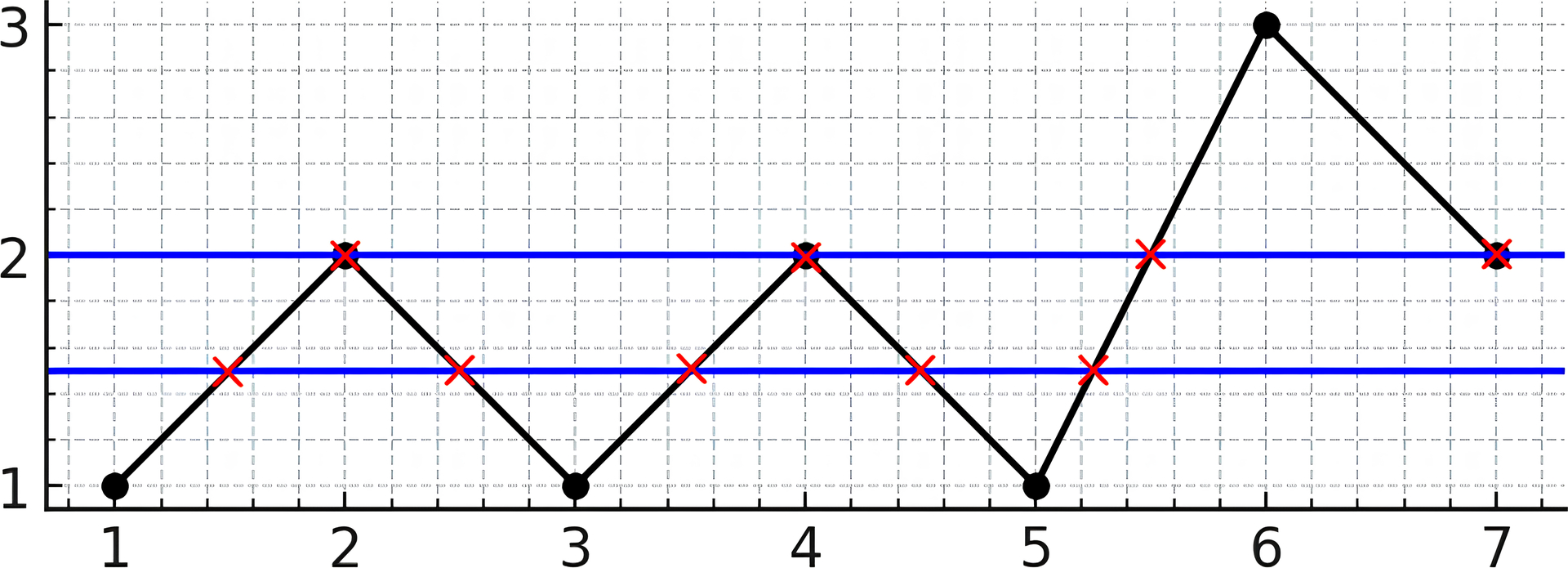
输入：y = [1,2,1,2,1,3,2]
输出：5
解释：如上图所示，水平线 y = 1.5 与折线相交了 5 次（用红叉表示）。水平线 y = 2 与折线相交了 4 次（用红叉表示）。可以证明没有其他水平线可以与折线有超过 5 个点相交。因此，答案是 5。

示例 2：

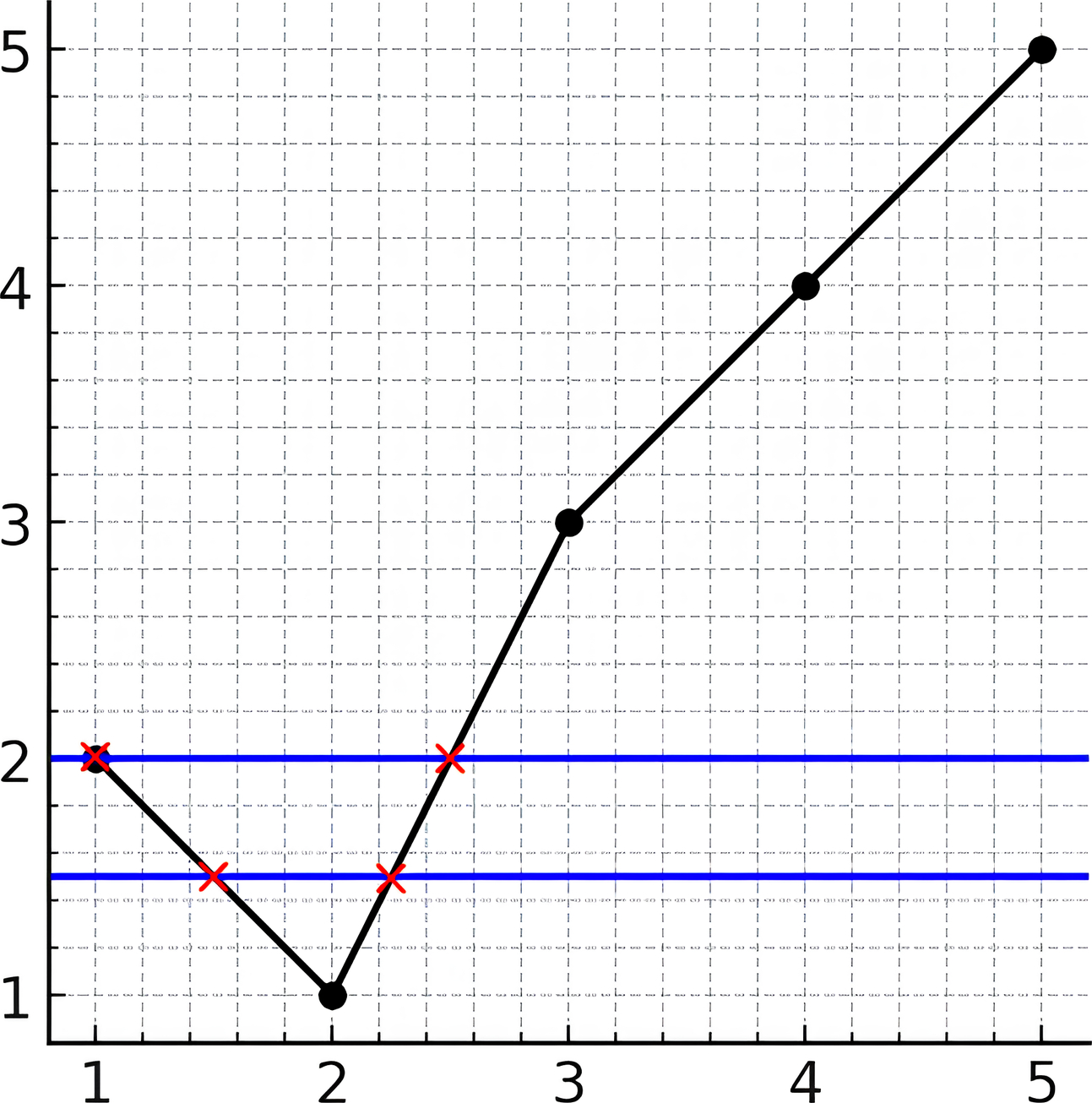
输入：y = [2,1,3,4,5]
输出：2
解释：如上图所示，水平线 y=1.5 与折线相交了 2 次（用红叉表示）。水平线 y=2 与折线相交了 2 次（用红叉表示）。可以证明没有其他水平线可以与折线有超过 2 个点相交。因此，答案是 2。

提示：

• 2 <= y.length <= 105
• 1 <= y[i] <= 109
• 对于范围 [1, n - 1] 内的所有 i，都有 y[i] != y[i + 1]

分析

• 由于最优的线可能在两点之间，不为整数，考虑将所有 y 坐标乘 2，保证最优线为整数
• 然后可以用差分，从 y1 到 y2 的折线，等同于将区间 [y1,y2] 加 1
• 注意不能重复统计，比如连续的 y1,y2,y3 的折线，y2 不能加两次

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution:
    def maxIntersectionCount(self, y: List[int]) -> int:
        d = defaultdict(int)
        y = [a*2 for a in y]
        d[y[0]] += 1
        d[y[0]+1] -= 1
        for a,b in pairwise(y):
            a,b = (a+1,b) if a<b else (b,a-1)
            d[a] += 1
            d[b+1] -= 1
        res,s = 0,0
        for x in sorted(d): 
            s += d[x]
            res = max(res,s)
        return res

579 ms