2792：计算足够大的节点数（★★）

力扣第 2792 题

题目

给定一棵二叉树的根节点 root 和一个整数 k 。如果一个节点满足以下条件，则称其为 足够大 ：

• 它的子树中 至少 有 k 个节点。
• 它的值 大于 其子树中 至少 k 个节点的值。

返回足够大的节点数。

如果 u == v 或者 v 是 u 的祖先，则节点 u 在节点 v 的 子树 中。

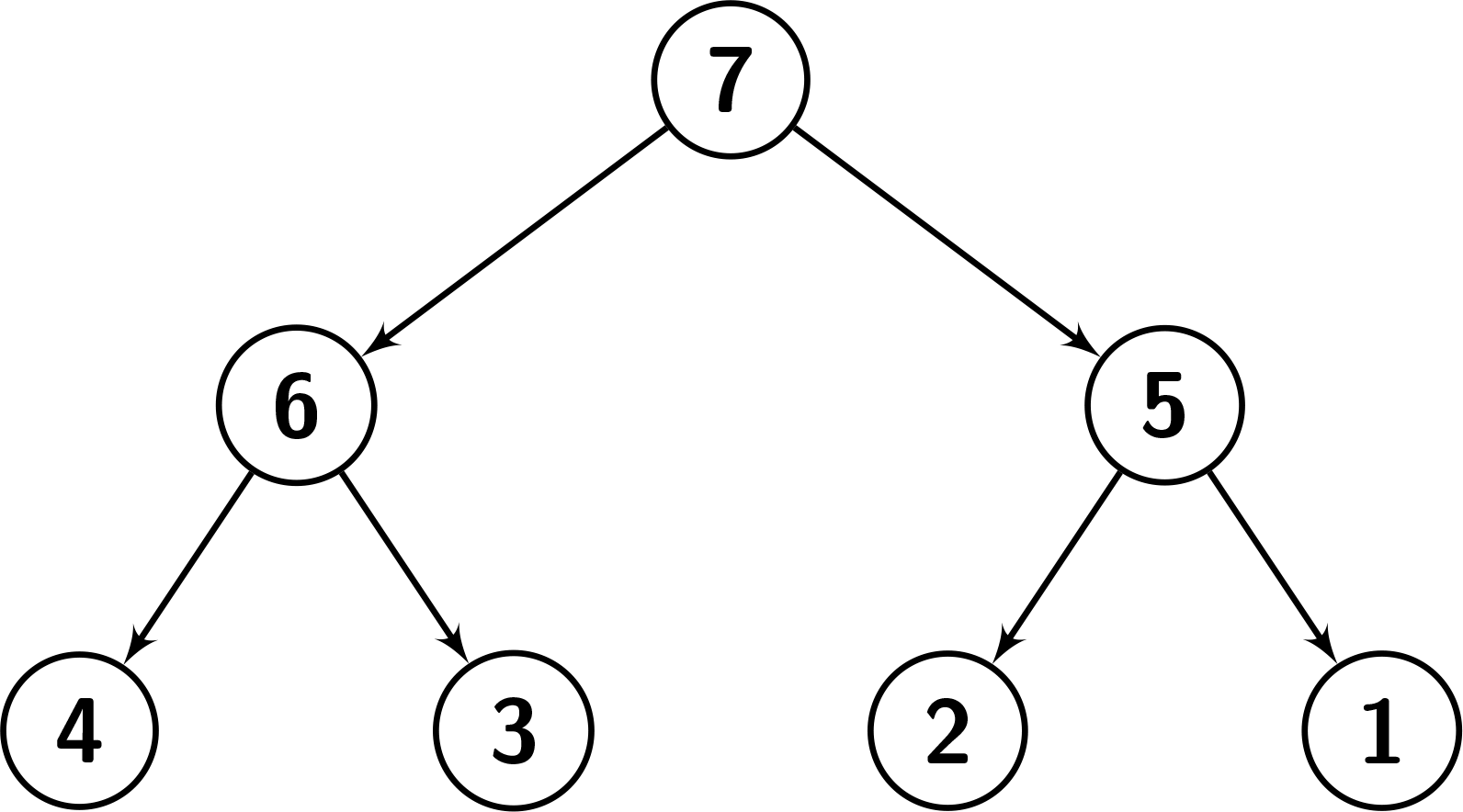
示例 1：

输入：root = [7,6,5,4,3,2,1], k = 2
输出：3
解释：节点编号从 1 到 7。
节点 1 的子树中的值：{1,2,3,4,5,6,7}。由于节点的值等于 7，有 6 个节点的值小于它的值，因此它是“足够大”的。
节点 2 的子树中的值：{3,4,6}。由于节点的值等于 6，有 2 个节点的值小于它的值，因此它是“足够大”的。
节点 3 的子树中的值：{1,2,5}。由于节点的值等于 5，有 2 个节点的值小于它的值，因此它是“足够大”的。
其他节点不满足条件。
参考下面的图片可以帮助你得到更好的理解。

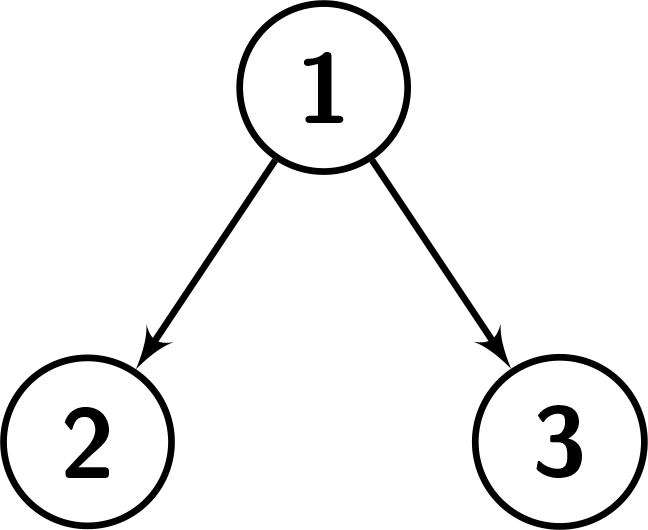
示例 2：

输入：root = [1,2,3], k = 1
输出：0
解释：节点编号从 1 到 3。
节点 1 的子树中的值：{1,2,3}。由于节点的值等于 1，没有节点的值小于它的值，因此它不是“足够大”的。
节点 2 的子树中的值：{2}。由于节点的值等于 2，没有节点的值小于它的值，因此它不是“足够大”的。
节点 3 的子树中的值：{3}。由于节点的值等于 3，没有节点的值小于它的值，因此它不是“足够大”的。
参考下面的图片可以帮助你得到更好的理解。

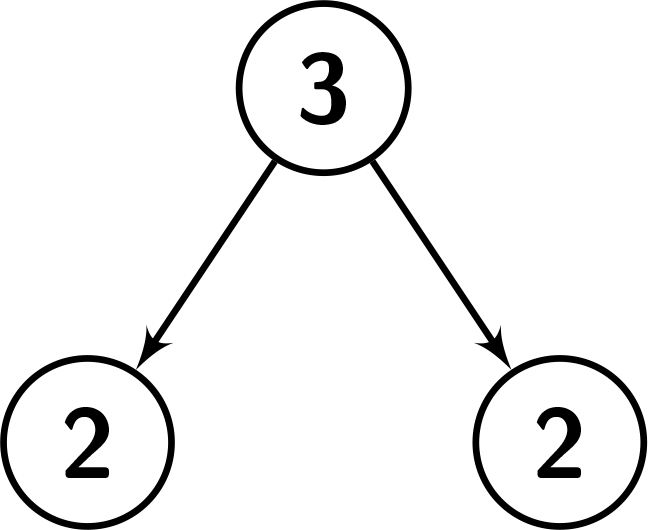
示例 3：

输入：root = [3,2,2], k = 2
输出：1
解释：节点编号从 1 到 3。
节点 1 的子树中的值：{2,2,3}。
由于节点的值等于 3，有 2 个节点的值小于它的值，因此它是“足够大”的。
节点 2 的子树中的值：{2}。由于节点的值等于 2，没有节点的值小于它的值，因此它不是“足够大”的。
节点 3 的子树中的值：{2}。由于节点的值等于 2，没有节点的值小于它的值，因此它不是“足够大”的。
参考下面的图片可以帮助你得到更好的理解。

提示：

• 树中的节点数在范围 [1, 104] 内。
• 1 <= Node.val <= 104
• 1 <= k <= 10

分析

• 子树返回前 k 小的节点值即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution:
    def countGreatEnoughNodes(self, root: Optional[TreeNode], k: int) -> int:
        res = 0
        def dfs(u):
            A = [u.val]
            for v in [u.left,u.right]:
                if v:
                    A = nsmallest(k,A+dfs(v))
            nonlocal res
            if u.val>A[-1]:
                res += 1
            return A
        dfs(root)
        return res 

675 ms