2714：找到 K 次跨越的最短路径（★★）

2023-05-29 约 1264 字预计阅读 3 分钟次阅读

力扣第 2714 题

题目

现给定一个正整数 n ，它表示一个 索引从 0 开始的无向带权连接图 的节点数，以及一个 索引从 0 开始的二维数组 edges ，其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间存在权重为 wi 的边。

还给定两个节点 s 和 d ，以及一个正整数 k ，你的任务是找到从 s 到 d 的最短路径，但你可以最多跨越 k 条边。换句话说，将最多 k 条边的权重设为 0，然后找到从 s 到 d 的最短路径。

返回满足给定条件的从 s 到 d 的最短路径的长度。

示例 1：

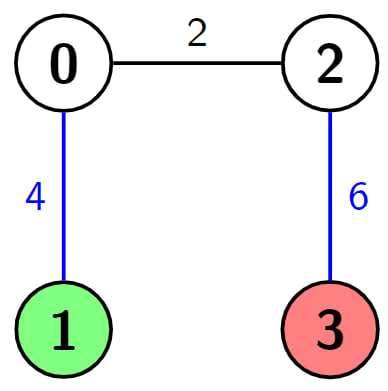
输入：n = 4, edges = [[0,1,4],[0,2,2],[2,3,6]], s = 1, d = 3, k = 2
输出：2
解释：在这个例子中，只有一条从节点1（绿色节点）到节点3（红色节点）的路径，即（1->0->2->3），其长度为4 + 2 + 6 = 12。现在我们可以将两条边的权重设为 0，即将蓝色边的权重设为 0，那么路径的长度就变为 0 + 2 + 0 = 2。可以证明 2 是我们在给定条件下能够达到的最小路径长度。

示例 2：

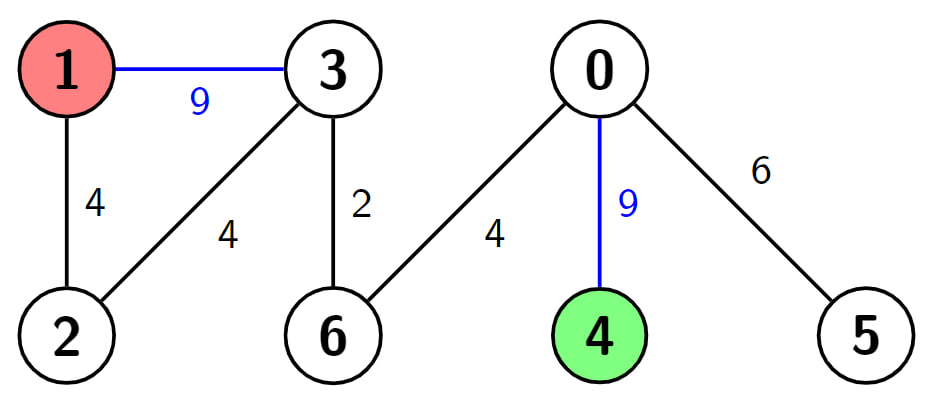
输入：n = 7, edges = [[3,1,9],[3,2,4],[4,0,9],[0,5,6],[3,6,2],[6,0,4],[1,2,4]], s = 4, d = 1, k = 2
输出：6
解释：在这个例子中，有两条从节点4（绿色节点）到节点1（红色节点）的路径，分别是（4->0->6->3->2->1）和（4->0->6->3->1）。第一条路径的长度为 9 + 4 + 2 + 4 + 4 = 23，第二条路径的长度为 9 + 4 + 2 + 9 = 24。现在，如果我们将蓝色边的权重设为 0，那么最短路径的长度就变为 0 + 4 + 2 + 0 = 6。可以证明 6 是我们在给定条件下能够达到的最小路径长度。

示例 3：

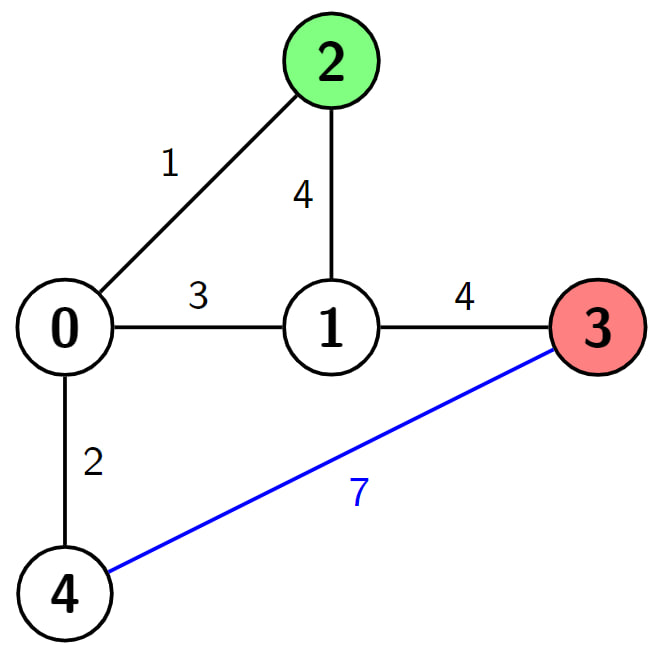
输入：n = 5, edges = [[0,4,2],[0,1,3],[0,2,1],[2,1,4],[1,3,4],[3,4,7]], s = 2, d = 3, k = 1
输出：3
解释：在这个例子中，从节点2（绿色节点）到节点3（红色节点）有4条路径，分别是（2->1->3）、（2->0->1->3）、（2->1->0->4->3）和（2->0->4->3）。前两条路径的长度为4 + 4 = 1 + 3 + 4 = 8，第三条路径的长度为4 + 3 + 2 + 7 = 16，最后一条路径的长度为1 + 2 + 7 = 10。现在，如果我们将蓝色边的权重设为 0，那么最短路径的长度就为1 + 2 + 0 = 3。可以证明在给定条件下，3 是我们能够达到的最小路径长度。

提示：

2 <= n <= 500
n - 1 <= edges.length <= n * (n - 1) / 2
edges[i].length = 3
0 <= edges[i][0], edges[i][1] <= n - 1
1 <= edges[i][2] <= 10⁶
0 <= s, d, k <= n - 1
s != d
输入的生成确保图是连通的，并且没有 重复的边 或自环。

分析

#1

令状态 <u,i> 代表到达节点 u，跨越了 i 次，dijkstra 跑最短路即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


class Solution:
    def shortestPathWithHops(self, n: int, edges: List[List[int]], s: int, d: int, k: int) -> int:
        g = [[] for _ in range(n)]
        for u,v,w in edges:
            g[u].append((v,w))
            g[v].append((u,w))
        f = [[inf]*(k+1) for _ in range(n)]
        f[s][0] = 0
        pq = [(0,s,0)]
        while pq:
            w,u,i = heappop(pq)
            if u==d:
                return w
            if w>f[u][i]:
                continue
            for v,w2 in g[u]:
                if w+w2<f[v][i]:
                    f[v][i] = w+w2
                    heappush(pq,(w+w2,v,i))
                if i<k and w<f[v][i+1]:
                    f[v][i+1] = w
                    heappush(pq,(w,v,i+1))

559 ms

#2

注意到对于 <w1,u,i1>,<w2,u,i2>，若 w1<=w2 且 i1<=i2，则 <w2,u,i2> 无需再考虑
因此可以新增数组 T 存储 u 对应的 i，限制状态

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


class Solution:
    def shortestPathWithHops(self, n: int, edges: List[List[int]], s: int, d: int, k: int) -> int:
        g = [[] for _ in range(n)]
        for u,v,w in edges:
            g[u].append((v,w))
            g[v].append((u,w))
        f = [[inf]*(k+1) for _ in range(n)]
        f[s][0] = 0
        T = [inf]*n
        pq = [(0,s,0)]
        while pq:
            w,u,i = heappop(pq)
            if u==d:
                return w
            if w>f[u][i] or i>=T[u]:
                continue
            T[u] = i
            for v,w2 in g[u]:
                if w+w2<f[v][i]:
                    f[v][i] = w+w2
                    heappush(pq,(w+w2,v,i))
                if i<k and w<f[v][i+1]:
                    f[v][i+1] = w
                    heappush(pq,(w,v,i+1))

104 ms

目录

2714：找到 K 次跨越的最短路径（★★）

题目

分析

#1

#2

解答