2647：把三角形染成红色（★★）

力扣第 2647 题

题目

现给定你一个整数 n 。考虑一个边长为 n 的等边三角形，被分成 n2 个单位等边三角形。这个三角形有 n 个 从 1 开始编号 的行，其中第 i 行有 2i - 1 个单位等边三角形。

第 i 行的三角形也是 从 1 开始编号 的，其坐标从 (i, 1) 到 (i, 2i - 1) 。下面的图像显示了一个边长为 4 的三角形及其三角形的索引。

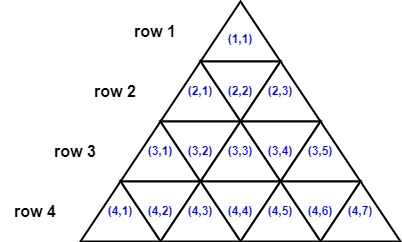
如果两个三角形 共享一条边 ，则它们是 相邻 的。例如：

• 三角形 (1,1) 和 (2,2) 是相邻的。
• 三角形 (3,2) 和 (3,3) 是相邻的。
• 三角形 (2,2) 和 (3,3) 不相邻，因为它们没有共享任何边。

初始时，所有单位三角形都是 白色 的。你想选择 k 个三角形并将它们涂成 红色 。然后我们将运行以下算法：

1. 选择一个 至少有两个 红色相邻三角形的白色三角形。
   • 如果没有这样的三角形，请停止算法。
2. 将该三角形涂成 红色 。
3. 回到步骤 1。

选择最小的 k 并在运行此算法之前将 k 个三角形涂成红色，使得在算法停止后，所有单元三角形都被涂成红色。

返回一个二维列表，其中包含你要最初涂成红色的三角形的坐标。答案必须尽可能小。如果有多个有效的解决方案，请返回其中任意一个。

示例 1 ：

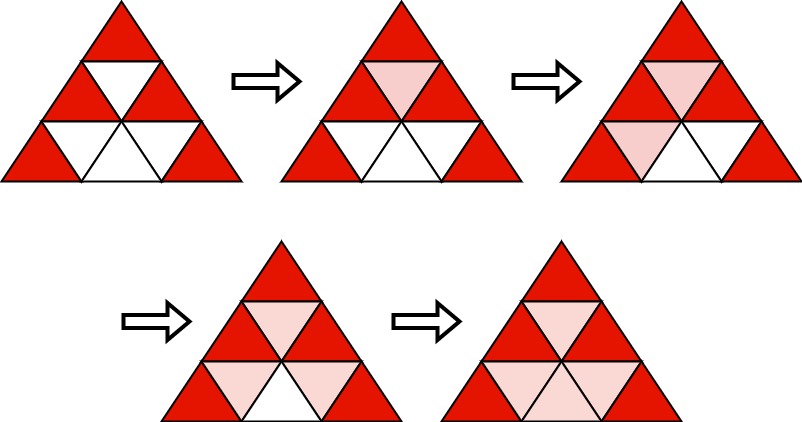
输入：n = 3
输出：[[1,1],[2,1],[2,3],[3,1],[3,5]]
解释：初始时，我们选择展示的5个三角形染成红色。然后，我们运行以下算法：
- 选择(2,2)，它有三个红色相邻的三角形，并将其染成红色。
- 选择(3,2)，它有两个红色相邻的三角形，并将其染成红色。
- 选择(3,4)，它有三个红色相邻的三角形，并将其染成红色。
- 选择(3,3)，它有三个红色相邻的三角形，并将其染成红色。
可以证明，选择任何4个三角形并运行算法都无法将所有三角形都染成红色。

示例 2 ：

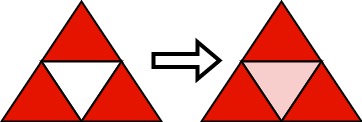
输入：n = 2
输出：[[1,1],[2,1],[2,3]]
解释：初始时，我们选择图中所示的 3 个三角形为红色。然后，我们运行以下算法：
-选择有三个红色相邻的 (2,2) 三角形并将其染成红色。
可以证明，选择任意 2 个三角形并运行该算法都不能使所有三角形变为红色。

提示：

• 1 <= n <= 1000

分析

• 同 lcp70 相同

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution:
    def colorRed(self, n: int) -> List[List[int]]:
        res = [[1,1]]
        for i in range(n,1,-1):
            r = (n-i)%4
            if r==0:
                res.extend([i,j*2+1] for j in range(i))
            elif r==1:
                res.append([i,2])
            elif r==2:
                res.extend([i,j*2+1] for j in range(1,i))
            else:
                res.append([i,1])
        return res

79 ms