力扣第 2479 题
题目
有一个无向树,有 n 个节点,节点标记为从 0 到 n - 1。给定整数 n 和一个长度为 n - 1 的 2 维整数数组 edges,其中 edges[i] = [ai, bi] 表示在树中的节点 ai 和 bi 之间有一条边。树的根节点是标记为 0 的节点。
每个节点都有一个相关联的 值。给定一个长度为 n 的数组 values,其中 values[i] 是第 i 个节点的 值。
选择任意两个 不重叠 的子树。你的 分数 是这些子树中值的和的逐位异或。
返回你能达到的最大分数。如果不可能找到两个不重叠的子树,则返回 0。
注意:
- 节点的 子树 是由该节点及其所有子节点组成的树。
- 如果两个子树不共享 任何公共 节点,则它们是 不重叠 的。
示例 1:
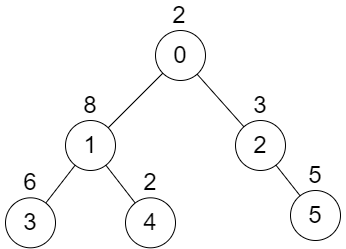
输入: n = 6, edges = [[0,1],[0,2],[1,3],[1,4],[2,5]], values = [2,8,3,6,2,5]
输出: 24
解释: 节点 1 的子树的和值为 16,而节点 2 的子树的和值为 8,因此选择这些节点将得到 16 XOR 8 = 24 的分数。可以证明,这是我们能得到的最大可能分数。
示例 2:
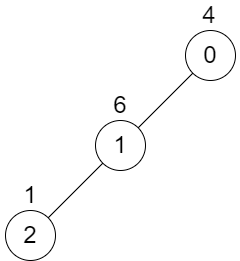
输入: n = 3, edges = [[0,1],[1,2]], values = [4,6,1]
输出: 0
解释: 不可能选择两个不重叠的子树,所以我们只返回 0。
提示:
2 <= n <= 5 * 104edges.length == n - 10 <= ai, bi < nvalues.length == n1 <= values[i] <= 109- 保证
edges 代表一个有效的树。
分析
- 异或对问题常用 01字典树
- 为了保证不重叠,dfs 进入时进行计算,返回时才将值添加到字典树中
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
# 01字典树,基于数组
class BitTrie:
def __init__(self,n,L): # 插入总长度 n、最长 L 的二进制串
self.t = [[0]*(n+1) for _ in range(2)]
self.s = [0]*(n+1)
self.L = L
self.i = 0
def add(self, x):
p = 0
for j in range(self.L-1, -1, -1):
b = (x>>j)&1
if not self.t[b][p]:
self.t[b][p] = self.i = self.i+1
p = self.t[b][p]
self.s[p] += 1
def remove(self,x):
p = 0
for j in range(self.L-1,-1,-1):
b = (x>>j)&1
p = self.t[b][p]
self.s[p] -= 1
def maxxor(self,x): # 树中与 x 异或的最大值
res = 0
p = 0
for j in range(self.L-1, -1, -1):
b = (x>>j)&1
q = self.t[b^1][p]
if q and self.s[q]:
res |= 1 << j
b ^= 1
p = self.t[b][p]
return res
class Solution:
def maxXor(self, n: int, edges: List[List[int]], values: List[int]) -> int:
g = [[] for _ in range(n)]
for u,v in edges:
g[u].append(v)
g[v].append(u)
f = values[:]
def dfs(u,fa):
for v in g[u]:
if v!=fa:
dfs(v,u)
f[u] += f[v]
dfs(0,-1)
L = f[0].bit_length()
trie = BitTrie(n*L,L)
res = 0
def dfs(u,fa):
nonlocal res
res = max(res,trie.maxxor(f[u]))
for v in g[u]:
if v!=fa:
dfs(v,u)
trie.add(f[u])
dfs(0,-1)
return res
|
730 ms

