2277：树中最接近路径的节点（★★）

2022-05-16 约 847 字预计阅读 2 分钟次阅读

力扣第 2277 题

题目

给定一个正整数 n，表示树中的节点数，编号从 0 到 n - 1 (含边界)。还给定一个长度为 n - 1 的二维整数数组 edges，其中 edges[i] = [node1_i, node2_i] 表示有一条双向边连接树中的 node1_i 和 node2_i。

给定一个长度为 m ，下标从 0 开始 的整数数组 query，其中 query[i] = [start_i, end_i, node_i] 意味着对于第 i 个查询，您的任务是从 start_i 到 end_i 的路径上找到 最接近 node_i的节点。

返回长度为 m 的整数数组 answer，其中 answer[i] 是第 i 个查询的答案。

示例 1:

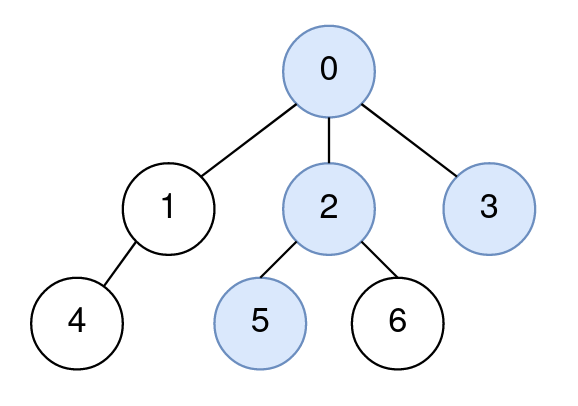
输入: n = 7, edges = [[0,1],[0,2],[0,3],[1,4],[2,5],[2,6]], query = [[5,3,4],[5,3,6]]
输出: [0,2]
解释:
节点 5 到节点 3 的路径由节点 5、2、0、3 组成。
节点 4 到节点 0 的距离为 2。
节点 0 是距离节点 4 最近的路径上的节点，因此第一个查询的答案是 0。
节点 6 到节点 2 的距离为 1。
节点 2 是距离节点 6 最近的路径上的节点，因此第二个查询的答案是 2。

示例 2:

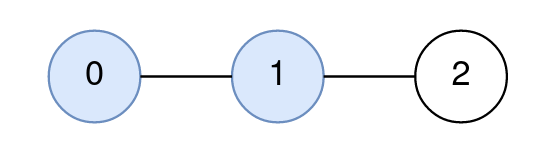
输入: n = 3, edges = [[0,1],[1,2]], query = [[0,1,2]]
输出: [1]
解释:
从节点 0 到节点 1 的路径由节点 0,1 组成。
节点 2 到节点 1 的距离为 1。
节点 1 是距离节点 2 最近的路径上的节点，因此第一个查询的答案是 1。

示例 3:

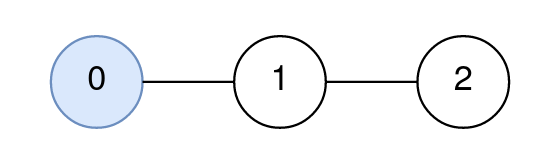
输入: n = 3, edges = [[0,1],[1,2]], query = [[0,0,0]]
输出: [0]
解释:
节点 0 到节点 0 的路径由节点 0 组成。
因为 0 是路径上唯一的节点，所以第一个查询的答案是0。

提示:

1 <= n <= 1000
edges.length == n - 1
edges[i].length == 2
0 <= node1_i, node2_i <= n - 1
node1_i != node2_i
1 <= query.length <= 1000
query[i].length == 3
0 <= start_i, end_i, node_i <= n - 1
这个图是一个树。

相似问题：

分析

等价于找三条路径的交点
一种方法是分别求出 a=lca(x,y),b=lca(x,z),c=lca(y,z)，a^b^c 即是交点

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51


# 倍增求 lca
class LCA:
    def __init__(self,edges):
        n = len(edges)+1
        m = n.bit_length()
        g = [[] for _ in range(n)]
        for u,v in edges: 
            g[u].append(v)
            g[v].append(u)
        self.D = D = [0]*n
        self.f = f = [[-1]*m for _ in range(n)]
        sk = [0]
        while sk:
            u = sk.pop()
            for v in g[u]:
                if v!=f[u][0]:
                    sk.append(v)
                    f[v][0] = u
                    D[v] = D[u]+1
        for i in range(m-1):
            for u in range(n):
                p = f[u][i]
                if p!=-1:
                    f[u][i+1] = f[p][i]
    
    def kth(self,x,k):
        for i in range(k.bit_length()):
            if k>>i&1:
                x = self.f[x][i]
        return x
    
    def get(self,x,y):
        f,D = self.f,self.D
        if D[x]>D[y]:
            x,y = y,x
        y = self.kth(y,D[y]-D[x])
        if x!=y:
            for i in range(len(f[x])-1,-1,-1):
                px,py = f[x][i],f[y][i]
                if px!=py:
                    x,y = px,py
            x = f[x][0]
        return x

class Solution:
    def closestNode(self, n: int, edges: List[List[int]], query: List[List[int]]) -> List[int]:
        def cal(u,v,x):
            a,b,c = lca.get(u,v),lca.get(u,x),lca.get(v,x)
            return a^b^c
        lca = LCA(edges)
        return [cal(u,v,x) for u,v,x in query]

16 ms

目录

2277：树中最接近路径的节点（★★）

题目

分析

解答