1993:树上的操作(1861 分)
目录
题目
给你一棵 n 个节点的树,编号从 0 到 n - 1 ,以父节点数组 parent 的形式给出,其中 parent[i] 是第 i 个节点的父节点。树的根节点为 0 号节点,所以 parent[0] = -1 ,因为它没有父节点。你想要设计一个数据结构实现树里面对节点的加锁,解锁和升级操作。
数据结构需要支持如下函数:
- Lock:指定用户给指定节点 上锁 ,上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下,才能进行上锁操作。
- Unlock:指定用户给指定节点 解锁 ,只有当指定节点当前正被指定用户锁住时,才能执行该解锁操作。
- Upgrade:指定用户给指定节点 上锁 ,并且将该节点的所有子孙节点 解锁 。只有如下 3 个条件 全部 满足时才能执行升级操作:
- 指定节点当前状态为未上锁。
- 指定节点至少有一个上锁状态的子孙节点(可以是 任意 用户上锁的)。
- 指定节点没有任何上锁的祖先节点。
请你实现 LockingTree 类:
LockingTree(int[] parent)用父节点数组初始化数据结构。lock(int num, int user)如果 id 为user的用户可以给节点num上锁,那么返回true,否则返回false。如果可以执行此操作,节点num会被 id 为user的用户 上锁 。unlock(int num, int user)如果 id 为user的用户可以给节点num解锁,那么返回true,否则返回false。如果可以执行此操作,节点num变为 未上锁 状态。upgrade(int num, int user)如果 id 为user的用户可以给节点num升级,那么返回true,否则返回false。如果可以执行此操作,节点num会被 升级 。
示例 1:
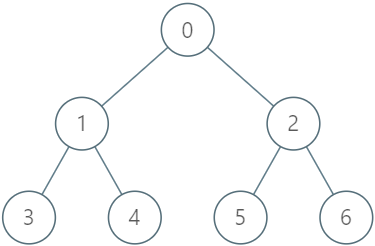
输入: ["LockingTree", "lock", "unlock", "unlock", "lock", "upgrade", "lock"] [[[-1, 0, 0, 1, 1, 2, 2]], [2, 2], [2, 3], [2, 2], [4, 5], [0, 1], [0, 1]] 输出: [null, true, false, true, true, true, false] 解释: LockingTree lockingTree = new LockingTree([-1, 0, 0, 1, 1, 2, 2]); lockingTree.lock(2, 2); // 返回 true ,因为节点 2 未上锁。 // 节点 2 被用户 2 上锁。 lockingTree.unlock(2, 3); // 返回 false ,因为用户 3 无法解锁被用户 2 上锁的节点。 lockingTree.unlock(2, 2); // 返回 true ,因为节点 2 之前被用户 2 上锁。 // 节点 2 现在变为未上锁状态。 lockingTree.lock(4, 5); // 返回 true ,因为节点 4 未上锁。 // 节点 4 被用户 5 上锁。 lockingTree.upgrade(0, 1); // 返回 true ,因为节点 0 未上锁且至少有一个被上锁的子孙节点(节点 4)。 // 节点 0 被用户 1 上锁,节点 4 变为未上锁。 lockingTree.lock(0, 1); // 返回 false ,因为节点 0 已经被上锁了。
提示:
n == parent.length2 <= n <= 2000- 对于
i != 0,满足0 <= parent[i] <= n - 1 parent[0] == -10 <= num <= n - 11 <= user <= 104parent表示一棵合法的树。lock,unlock和upgrade的调用 总共 不超过2000次。
相似问题:
分析
用 state 数组保存每个节点的 <是否上锁,上锁的用户 id>,然后模拟即可。
upgrade 时向上 dfs 确定没有上锁的祖先节点,然后向下 dfs 找所有上锁的子孙节点, 如果非空即代表符合条件,将它们解锁。
解答
|
|
1676 ms