1975：最大方阵和（1648 分）

力扣第 59 场双周赛第 2 题

题目

给你一个 n x n 的整数方阵 matrix 。你可以执行以下操作 任意次 ：

• 选择 matrix 中 相邻 两个元素，并将它们都 乘以 -1 。

如果两个元素有 公共边 ，那么它们就是 相邻 的。

你的目的是 最大化 方阵元素的和。请你在执行以上操作之后，返回方阵的 最大 和。

示例 1：

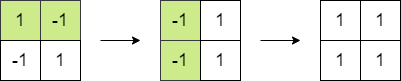
输入：matrix = [[1,-1],[-1,1]]
输出：4
解释：我们可以执行以下操作使和等于 4 ：
- 将第一行的 2 个元素乘以 -1 。
- 将第一列的 2 个元素乘以 -1 。

示例 2：

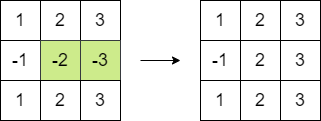
输入：matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
输出：16
解释：我们可以执行以下操作使和等于 16 ：
- 将第二行的最后 2 个元素乘以 -1 。

提示：

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -105 <= matrix[i][j] <= 105

分析

• 通过多次操作可以等价于将任意两个数同时乘以 -1
• 因此统计负数个数，若偶数个，可以全部转正
• 若奇数个，可以选一个绝对值最小的数作为唯一的负数

解答

1
2
3
4
5
6
7

class Solution:
    def maxMatrixSum(self, matrix: List[List[int]]) -> int:
        A = [abs(x) for row in matrix for x in row]
        c = sum(x<0 for row in matrix for x in row)
        if c%2==0:
            return sum(A)
        return sum(A)-min(A)*2

49 ms