1954:收集足够苹果的最小花园周长(1758 分)
目录
题目
给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。
你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。
给你一个整数 neededApples ,请你返回土地的 最小周长 ,使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。
|x| 的值定义为:
- 如果
x >= 0,那么值为x - 如果
x < 0,那么值为-x
示例 1:
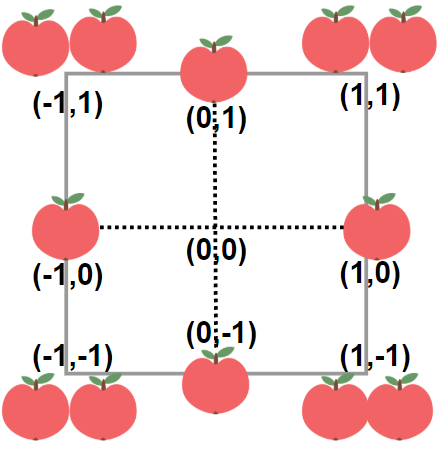
输入:neededApples = 1 输出:8 解释:边长长度为 1 的正方形不包含任何苹果。 但是边长为 2 的正方形包含 12 个苹果(如上图所示)。 周长为 2 * 4 = 8 。
示例 2:
输入:neededApples = 13 输出:16
示例 3:
输入:neededApples = 1000000000 输出:5040
提示:
1 <= neededApples <= 1015
分析
假设右上角坐标为 (n,n),可以分别计算横纵坐标之和:
- 每一行的横坐标都是从 -n 到 n,和为 n(n+1)
- 共 2n+1 行,故所有横坐标之和为 n(n+1)(2n+1)
- 纵坐标同理
然后求最小的 n 使得 $2n(n+1)(2n+1)<=neededApples$,即是典型的二分查找。
最后 8n 即是最小周长。
解答
|
|
52 ms