力扣第 249 场周赛第 3 题
题目
给你两个整数 m 和 n 。构造一个 m x n 的网格,其中每个单元格最开始是白色。请你用 红、绿、蓝 三种颜色为每个单元格涂色。所有单元格都需要被涂色。
涂色方案需要满足:不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大, 返回 对 109 + 7 取余 的结果。
示例 1:

输入:m = 1, n = 1
输出:3
解释:如上图所示,存在三种可能的涂色方案。
示例 2:
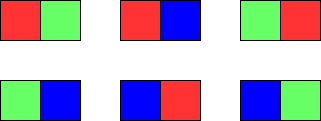
输入:m = 1, n = 2
输出:6
解释:如上图所示,存在六种可能的涂色方案。
示例 3:
输入:m = 5, n = 5
输出:580986
提示:
1 <= m <= 51 <= n <= 1000
相似问题:
分析
#1
- 注意 m 很小
- 令 f(i,st) 代表涂了前 i 列且第 i 列颜色状态为 st 的方法数,即可递推
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
mod = 10**9+7
class Solution:
def colorTheGrid(self, m: int, n: int) -> int:
valid = []
for A in product(range(3),repeat=m):
if all(a!=b for a,b in pairwise(A)):
valid.append(A)
N = len(valid)
g = [[] for _ in range(N)]
for i in range(N):
for j in range(N):
if all(a!=b for a,b in zip(valid[i],valid[j])):
g[i].append(j)
f = [1]*N
for _ in range(n-1):
nf = [0]*N
for i in range(N):
nf[i] = sum(f[j] for j in g[i])%mod
f = nf
return sum(f)%mod
|
219 ms
#2
- 还可以用矩阵快速幂优化
- m 很小,可以预处理每个 m 对应的递推式
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
|
# 矩阵快速幂优化
mod = 10**9+7
class MatPow:
def __init__(self,A): # k 阶递推式需要给定前 k*2 项
k = len(A)//2
self.f = A[:k]
self.A = A
self.g = self.gen(A)[::-1]
def gen(self,A): # Berlekamp-Massey 算法,给定前 k*2 项 A,返回符合的最短系数组 g
pre_c = []
pre_i, pre_d = -1, 0
g = []
for i,a in enumerate(A):
d = (a-sum(x*A[i-1-j] for j,x in enumerate(g)))%mod
if d == 0:
continue
if pre_i<0: # 首次算错,初始化 g 为 i+1 个 0
g = [0]*(i+1)
pre_i,pre_d = i,d
continue
bias = i-pre_i
old_len = len(g)
new_len = bias + len(pre_c)
if new_len>old_len: # 递推式变长了
tmp = g[:]
g += [0]*(new_len-old_len)
delta = d*pow(pre_d,-1,mod)%mod
g[bias-1] = (g[bias-1]+delta)%mod
for j,c in enumerate(pre_c):
g[bias+j] = (g[bias+j]-delta*c)%mod
if new_len>old_len:
pre_c = tmp
pre_i,pre_d = i,d
return g
def get(self,n): # Kitamasa 算法,给定前 k 项 f 和系数组 g,求第 n 项
def compose(A,B): # 根据 g(n) 的系数组 A 和 g(m) 的系数组 B 计算 g(n+m) 的系数组
C = [0]*k
for a in A:
for j,b in enumerate(B):
C[j] = (C[j]+a*b)%mod
B = [((B[i-1] if i else 0)+B[-1]*g[i])%mod for i in range(k)]
return C
f,g = self.f,self.g
if n<len(f):
return f[n]%mod
k = len(g)
if k == 0:
return 0
if k == 1:
return f[0]*pow(g[0],n,mod)%mod
res = [0]*k
C = [0]*k
res[0] = C[1] = 1
while n:
res = compose(C,res) if n&1 else res
C = compose(C,C)
n >>= 1
return sum(a*b for a,b in zip(res,f))%mod
MP = []
for m in range(1,6):
valid = []
for A in product(range(3),repeat=m):
if all(a!=b for a,b in pairwise(A)):
valid.append(A)
N = len(valid)
g = [[] for _ in range(N)]
for i in range(N):
for j in range(N):
if all(a!=b for a,b in zip(valid[i],valid[j])):
g[i].append(j)
A = [N]
f = [1]*N
for _ in range(N*2-1):
f = [sum(f[j] for j in g[i])%mod for i in range(N)]
A.append(sum(f)%mod)
MP.append(MatPow(A))
class Solution:
def colorTheGrid(self, m: int, n: int) -> int:
return MP[m-1].get(n-1)
|
0 ms

