1823:找出游戏的获胜者(1412 分)
目录
题目
共有 n 名小伙伴一起做游戏。小伙伴们围成一圈,按 顺时针顺序 从 1 到 n 编号。确切地说,从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置,其中 1 <= i < n ,从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。
游戏遵循如下规则:
- 从第
1名小伙伴所在位置 开始 。 - 沿着顺时针方向数
k名小伙伴,计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数,一些小伙伴可能会被数过不止一次。 - 你数到的最后一名小伙伴需要离开圈子,并视作输掉游戏。
- 如果圈子中仍然有不止一名小伙伴,从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始,回到步骤
2继续执行。 - 否则,圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ,和一个整数 k ,返回游戏的获胜者。
示例 1:
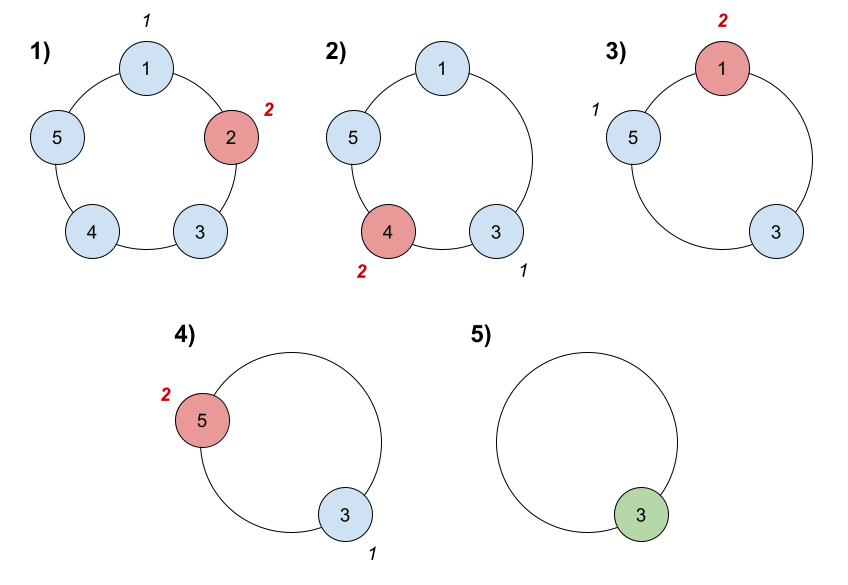
输入:n = 5, k = 2 输出:3 解释:游戏运行步骤如下: 1) 从小伙伴 1 开始。 2) 顺时针数 2 名小伙伴,也就是小伙伴 1 和 2 。 3) 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。 4) 顺时针数 2 名小伙伴,也就是小伙伴 3 和 4 。 5) 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。 6) 顺时针数 2 名小伙伴,也就是小伙伴 5 和 1 。 7) 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。 8) 顺时针数 2 名小伙伴,也就是小伙伴 3 和 5 。 9) 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。
示例 2:
输入:n = 6, k = 5 输出:1 解释:小伙伴离开圈子的顺序:5、4、6、2、3 。小伙伴 1 是游戏的获胜者。
提示:
1 <= k <= n <= 500
进阶:你能否使用线性时间复杂度和常数空间复杂度解决此问题?
分析
#1
经典的约瑟夫环问题。
方便起见,编号变为从 0 到 n-1,显然问题等价。
令 help(n) 代表 n 个人玩游戏的获胜者编号。第一轮后,相当于从编号 k 开始的 n-1 名小伙伴玩游戏,这是一个递归子问题。 设 help(n-1) 的获胜者编号为 x,那么 help(n) 的获胜者相当于从 k 开始的第 x 个,编号即为 (k+x)%n。
最简单的子问题即是 n=1 时,显然获胜者编号为 0。
最终 help(n)+1 即为所求。
|
|
40 ms
#2
可以改写成递推的形式。
解答
|
|
32 ms