1766：互质树（2231 分）

力扣第 46 场双周赛第 4 题

题目

给你一个 n 个节点的树（也就是一个无环连通无向图），节点编号从 0 到 n - 1 ，且恰好有 n - 1 条边，每个节点有一个值。树的 根节点 为 0 号点。

给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值，edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。

当 gcd(x, y) == 1 ，我们称两个数 x 和 y 是 互质的 ，其中 gcd(x, y) 是 x 和 y 的 最大公约数 。

从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。

请你返回一个大小为 n 的数组 ans ，其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的 ，如果不存在这样的祖先节点，ans[i] 为 -1 。

示例 1：

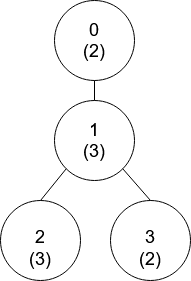
输入：nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出：[-1,0,0,1]
解释：上图中，每个节点的值在括号中表示。
- 节点 0 没有互质祖先。
- 节点 1 只有一个祖先节点 0 。它们的值是互质的（gcd(2,3) == 1）。
- 节点 2 有两个祖先节点，分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的（gcd(3,3) == 3）但节点 0 的值是互质的(gcd(2,3) == 1)，所以节点 0 是最近的符合要求的祖先节点。
- 节点 3 有两个祖先节点，分别是节点 1 和节点 0 。它与节点 1 互质（gcd(3,2) == 1），所以节点 1 是离它最近的符合要求的祖先节点。

示例 2：

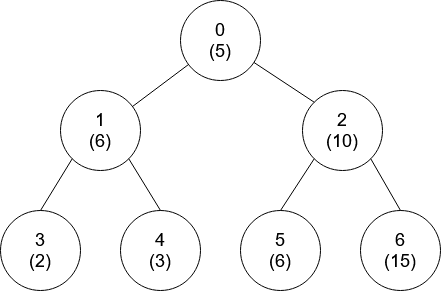
输入：nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出：[-1,0,-1,0,0,0,-1]

提示：

• nums.length == n
• 1 <= nums[i] <= 50
• 1 <= n <= 105
• edges.length == n - 1
• edges[j].length == 2
• 0 <= uj, vj < n
• uj != vj

分析

• 注意值的范围很小 1-50，因此遍历时维护当前每个值的最近祖先，比较即可
• 为了比较哪个最近，再维护深度即可
• 为了节省时间，可以提前打表 1-50 的互质关系

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

ma = 51
CP = [[y for y in range(1,ma) if gcd(x,y)==1] for x in range(ma)]

class Solution:
    def getCoprimes(self, nums: List[int], edges: List[List[int]]) -> List[int]:
        n = len(nums)
        g = defaultdict(list)
        for u,v in edges:
            g[u].append(v)
            g[v].append(u)
        A = [[(-1,-1)] for _ in range(ma)]
        ans = [-1]*len(nums)
        def dfs(u,f,h):
            x = nums[u]
            ans[u] = max(A[y][-1] for y in CP[x])[1]
            A[x].append((h,u))
            for v in g[u]:
                if v!=f:
                    dfs(v,u,h+1)
            A[x].pop()
        dfs(0,-1,0)
        return ans

713 ms