Ian
文章 动画 游戏 力扣 竞赛 关于
Ian

目录

1761：一个图中连通三元组的最小度数（2005 分）

   约 686 字   预计阅读 2 分钟    次阅读  

力扣第 228 场周赛第 4 题

题目

给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [ui, vi] ，表示 ui 和 vi 之间有一条无向边。

一个 连通三元组 指的是 三个 节点组成的集合且这三个点之间 两两 有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在这个三元组内，而另一个顶点不在这个三元组内。

请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

示例 1：

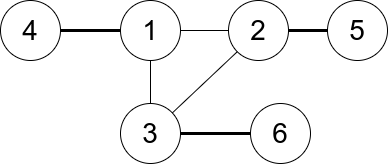
输入：n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
输出：3
解释：只有一个三元组 [1,2,3] 。构成度数的边在上图中已被加粗。

示例 2：

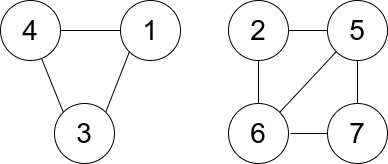
输入：n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
输出：0
解释：有 3 个三元组：
1) [1,4,3]，度数为 0 。
2) [2,5,6]，度数为 2 。
3) [5,6,7]，度数为 2 。

提示：

  • 2 <= n <= 400
  • edges[i].length == 2
  • 1 <= edges.length <= n * (n-1) / 2
  • 1 <= ui, vi <= n
  • ui != vi
  • 图中没有重复的边。

相似问题：

分析

#1

  • n 很小，暴力即可
  • 无向图统计节点集合的一个经典技巧是转为有向图
    • 将边的方向定为从度数小的点连向度数大的点（度数相等可以比较标号）
    • 边的出度最多 $O(\sqrt m)$
    • 枚举三元组即是 $O(m*\sqrt m)$
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution:
    def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:
        deg = Counter(x for p in edges for x in p)
        g = defaultdict(set)
        for u,v in edges:
            u,v = sorted([u,v],key=lambda x:[deg[x],x])
            g[u].add(v)
        res = inf
        for a in list(g):
            for b in g[a]:
                for c in g[b]:
                    if c in g[a]:
                        res = min(res,deg[a]+deg[b]+deg[c]-6)
        return res if res<inf else -1

3311 ms

#2

  • 集合可以用位运算优化
  • 注意到 a 和 b 的交集中，实际上只需要度数最小的点
  • 因此将点按度数大小离散化，再用位运算，直接取交集二进制状态的首位即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution:
    def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:
        deg = Counter(x for p in edges for x in p)
        A = sorted(range(1,n+1),key=lambda x:-deg[x])
        d = {a:i for i,a in enumerate(A)}
        g = defaultdict(int)
        for u,v in edges:
            u,v = sorted([d[u],d[v]])
            g[u] |= 1<<v
        res = inf
        for a in g:
            for b in g:
                if g[a]&1<<b and g[a]&g[b]:
                    c = (g[a]&g[b]).bit_length()-1
                    res = min(res,deg[A[a]]+deg[A[b]]+deg[A[c]]-6)
        return res if res<inf else -1

126 ms

更新于 2021-02-14
阅读原始文档
 困难, 图, 位运算, 优化
返回 | 主页