1632:矩阵转换后的秩(2529 分)
目录
题目
给你一个 m x n 的矩阵 matrix ,请你返回一个新的矩阵 answer ,其中 answer[row][col] 是 matrix[row][col] 的秩。
每个元素的 秩 是一个整数,表示这个元素相对于其他元素的大小关系,它按照如下规则计算:
- 秩是从 1 开始的一个整数。
- 如果两个元素
p和q在 同一行 或者 同一列 ,那么:- 如果
p < q,那么rank(p) < rank(q) - 如果
p == q,那么rank(p) == rank(q) - 如果
p > q,那么rank(p) > rank(q)
- 如果
- 秩 需要越 小 越好。
题目保证按照上面规则 answer 数组是唯一的。
示例 1:
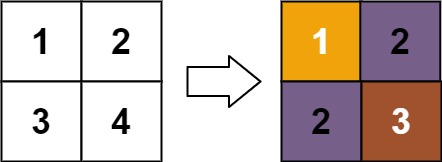
输入:matrix = [[1,2],[3,4]] 输出:[[1,2],[2,3]] 解释: matrix[0][0] 的秩为 1 ,因为它是所在行和列的最小整数。 matrix[0][1] 的秩为 2 ,因为 matrix[0][1] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。 matrix[1][0] 的秩为 2 ,因为 matrix[1][0] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。 matrix[1][1] 的秩为 3 ,因为 matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0] 且 matrix[0][1] 和 matrix[1][0] 的秩都为 2 。
示例 2:
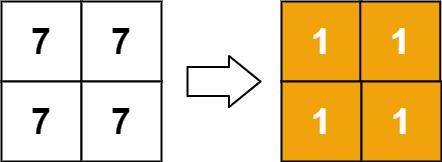
输入:matrix = [[7,7],[7,7]] 输出:[[1,1],[1,1]]
示例 3:
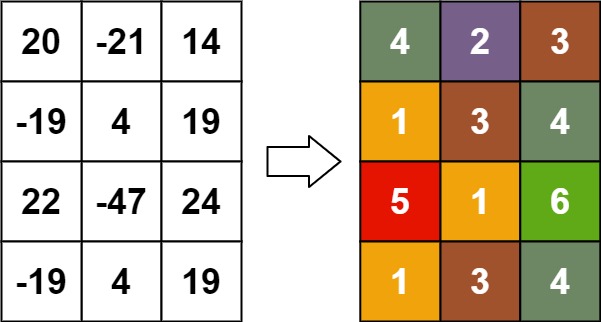
输入:matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]] 输出:[[4,2,3],[1,3,4],[5,1,6],[1,3,4]]
示例 4:
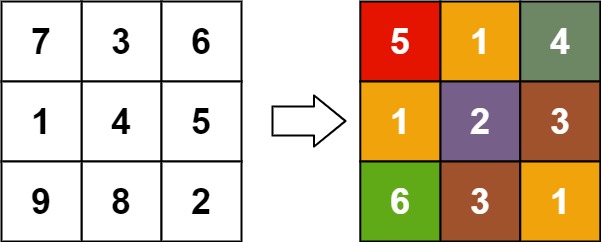
输入:matrix = [[7,3,6],[1,4,5],[9,8,2]] 输出:[[5,1,4],[1,2,3],[6,3,1]]
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 500-109 <= matrix[row][col] <= 109
相似问题:
分析
先考虑简化情形:没有相同的元素。那么显然最小的元素的秩为 1,第二小的元素则要考虑是否和最小元素同行或同列。 于是得到贪心解法:
从小到大遍历元素,并维护每行/列的最大秩,该元素的秩即为同行/列的最大秩加 1
存在相同元素时则较为复杂,假设两个相同元素同行/列,那么就要考虑到两个元素分别对应的 行/列 的最大秩。 同时还可能出现连动,比如元素 a 和 b 同行,b 和 c 同列,那么要同时考虑这三个元素。
这种连动容易想到并查集,于是用并查集将相同元素分为几个连通块,对于每个连通块, 里面所有元素对应的 行/列 最大秩 加 1,即为该连通块内所有元素的秩。
解答
|
|
1152 ms