1591：奇怪的打印机 II（2290 分）

Ian

2020-09-19 约 683 字预计阅读 2 分钟次阅读

力扣第 35 场双周赛第 4 题

题目

给你一个奇怪的打印机，它有如下两个特殊的打印规则：

每一次操作时，打印机会用同一种颜色打印一个矩形的形状，每次打印会覆盖矩形对应格子里原本的颜色。
一旦矩形根据上面的规则使用了一种颜色，那么 相同的颜色不能再被使用 。

给你一个初始没有颜色的 m x n 的矩形 targetGrid ，其中 targetGrid[row][col] 是位置 (row, col) 的颜色。

如果你能按照上述规则打印出矩形 targetGrid ，请你返回 true ，否则返回 false 。

示例 1：

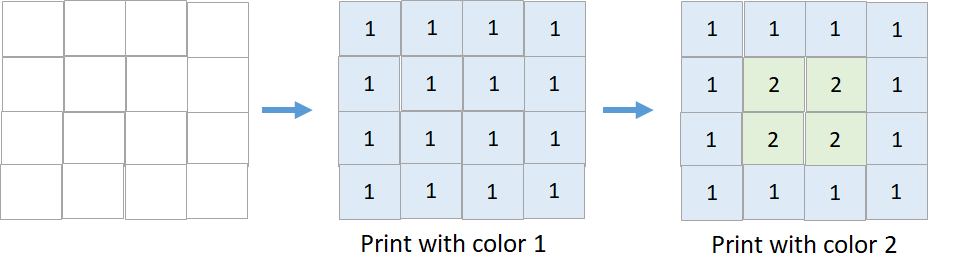
输入：targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
输出：true

示例 2：

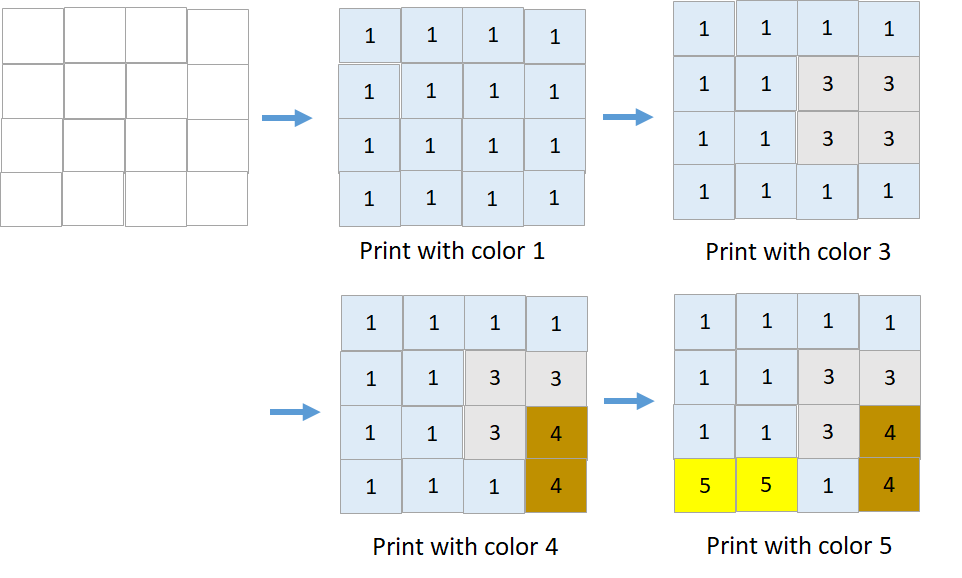
输入：targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
输出：true

示例 3：

输入：targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
输出：false
解释：没有办法得到 targetGrid ，因为每一轮操作使用的颜色互不相同。

示例 4：

输入：targetGrid = [[1,1,1],[3,1,3]]
输出：false

提示：

m == targetGrid.length
n == targetGrid[i].length
1 <= m, n <= 60
1 <= targetGrid[row][col] <= 60

相似问题：

分析

一种颜色只能打印一次，因此每种颜色打印的矩形必然包括了该颜色的所有点。

因此，某种颜色所有点的边界即对应了打印的矩形（更大没有意义）。确定了每种颜色的打印矩形，问题只在于打印顺序。

假如某个颜色 c 的矩形包含了其它颜色 c2，那么 c 必须在 c2 之前打印。如果不包含其它颜色，那么 c 可以最后打印。

于是转为拓扑排序问题，判断是否存在拓扑顺序即可。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


def isPrintable(self, targetGrid: List[List[int]]) -> bool:
    m, n = len(targetGrid), len(targetGrid[0])
    d = defaultdict(lambda: defaultdict(set))
    for i, j in product(range(m), range(n)):
        c = targetGrid[i][j]
        d[c]['X'].add(i)
        d[c]['Y'].add(j)
    nxt, indeg = defaultdict(set), defaultdict(int)
    for c in d:
        x1, x2 = min(d[c]['X']), max(d[c]['X'])
        y1, y2 = min(d[c]['Y']), max(d[c]['Y'])
        for x, y in product(range(x1, x2+1), range(y1, y2+1)):
            c2 = targetGrid[x][y]
            if c2 != c and c2 not in nxt[c]:
                nxt[c].add(c2)
                indeg[c2] += 1
    queue = deque(c for c in d if indeg[c]==0)
    while queue:
        u = queue.popleft()
        for v in nxt[u]:
            indeg[v] -= 1
            if indeg[v] == 0:
                queue.append(v)
    return all(indeg[c]==0 for c in d)

280 ms

目录

1591：奇怪的打印机 II（2290 分）

题目

分析

解答