力扣第 206 场周赛第 3 题
题目
给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。
示例 1：
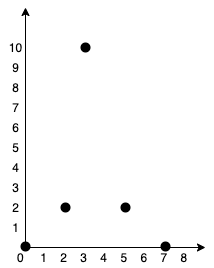
输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。
示例 2：
输入：points = [[3,12],[-2,5],[-4,1]]
输出：18
示例 3：
输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4
示例 4：
输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000
示例 5：
输入：points = [[0,0]]
输出：0
提示：
1 <= points.length <= 1000-106 <= xi, yi <= 106- 所有点
(xi, yi) 两两不同。
相似问题：
分析
#1
典型的最小生成树问题，按费用排序，依次判断是否添加边即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
def find(x):
if f[x] != x:
f[x] = find(f[x])
return f[x]
def union(x, y):
f[find(x)] = find(y)
def cal(p1, p2):
return abs(p1[0]-p2[0])+abs(p1[1]-p2[1])
n = len(points)
A = [[cal(points[i], points[j]), i, j] for i in range(n) for j in range(i+1, n)]
res, f = 0, list(range(n))
for w, i, j in sorted(A):
if find(i) != find(j):
union(i, j)
res += w
return res
|
2375 ms
#2
也可以用 prime 算法
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
def cal(p1, p2):
return abs(p1[0]-p2[0])+abs(p1[1]-p2[1])
n = len(points)
vis = [0]*n
d = [inf]*n
d[0] = 0
res = 0
for _ in range(n):
_,i = min((d[i],i) for i in range(n) if not vis[i])
res += d[i]
vis[i] = 1
for j in range(n):
if not vis[j]:
d[j] = min(d[j],cal(points[i],points[j]))
return res
|
595 ms