1514：概率最大的路径（1846 分）

力扣第 197 场周赛第 3 题

题目

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例 1：

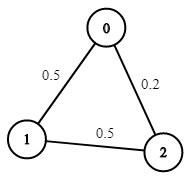
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

示例 2：

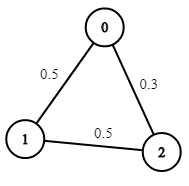
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出：0.30000

示例 3：

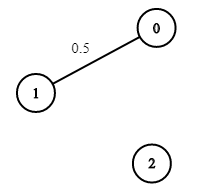
输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和 节点 2 之间不存在路径

提示：

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• 每两个节点之间最多有一条边

相似问题：

• 1976：到达目的地的方案数（2094 分）

分析

• 类似最短路，权重从相加改为了相乘，求的是最大
• 依然可以用 dijkstra 算法，初始权重设为 -1 即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution:
    def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start_node: int, end_node: int) -> float:
        g = [[] for _ in range(n)]
        for (a,b),p in zip(edges,succProb):
            g[a].append((b,p))
            g[b].append((a,p))
        d = [inf]*n
        d[start_node] = -1
        pq = [(-1,start_node)]
        while pq:
            w,u = heappop(pq)
            if w>d[u]:
                continue
            if u==end_node:
                return -w
            for v,w2 in g[u]:
                if w*w2<d[v]:
                    d[v]=w*w2
                    heappush(pq,(w*w2,v))
        return 0

129 ms