力扣第 28 场双周赛第 4 题
题目
给你一个房屋数组houses 和一个整数 k ,其中 houses[i] 是第 i 栋房子在一条街上的位置,现需要在这条街上安排 k 个邮筒。
请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。
答案保证在 32 位有符号整数范围以内。
示例 1:
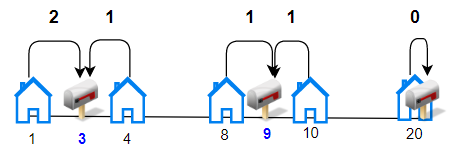
输入:houses = [1,4,8,10,20], k = 3
输出:5
解释:将邮筒分别安放在位置 3, 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。
示例 2:
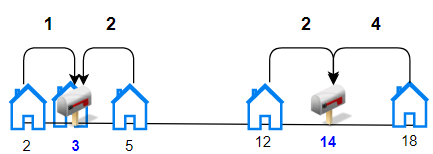
输入:houses = [2,3,5,12,18], k = 2
输出:9
解释:将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。
示例 3:
输入:houses = [7,4,6,1], k = 1
输出:8
示例 4:
输入:houses = [3,6,14,10], k = 4
输出:0
提示:
n == houses.length1 <= n <= 1001 <= houses[i] <= 10^41 <= k <= n- 数组
houses 中的整数互不相同。
分析
#1
- 令 f(i,j) 代表安排 i 个邮筒,houses[:j] 的最小距离和
- 遍历最后一个邮筒覆盖的房子范围 [a,j],转为子问题 f(i-1,a-1)
- 计算一个邮筒覆盖区间 [a,b] 的最小和,将邮筒放在区间中位数即可,可以预处理前缀和,快速计算得到
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution:
def minDistance(self, houses: List[int], k: int) -> int:
def w(a,b):
return p[b+1]-p[(a+b+1)//2]-(p[(a+b)//2+1]-p[a])
A = sorted(houses)
n = len(A)
p = [0]+list(accumulate(A))
f = [0]+[inf]*n
for i in range(1,k+1):
g = [0]+[inf]*n
for j in range(1,n+1):
for a in range(j):
g[j] = min(g[j],f[a]+w(a,j-1))
f = g
return f[-1]
|
520 ms
#2
- 区间代价函数 w 满足四边形不等式,可以利用决策单调性优化,详细见 四边形不等式优化
- 可以用分治,但更通用的是二分队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution:
def minDistance(self, houses: List[int], k: int) -> int:
def quad():
def w(a,b):
return f[a]+p[b]-p[(a+b)//2]-(p[(a+b+1)//2]-p[a])
g = [0]+[inf]*n
Q = deque([[0,1,n]])
for j in range(1,n+1):
while Q and Q[0][2]<j:
Q.popleft()
g[j] = w(Q[0][0],j)
while Q and w(j,Q[-1][1])<w(Q[-1][0],Q[-1][1]):
Q.pop()
if not Q:
Q.append([j,j+1,n])
else:
a = bisect_left(range(Q[-1][2]+1),True,j,key=lambda a:w(j,a)<w(Q[-1][0],a))
Q[-1][2] = a-1
if a<=n:
Q.append([j,a,n])
return g
A = sorted(houses)
n = len(A)
p = [0]+list(accumulate(A))
f = [0]+[inf]*n
for i in range(1,k+1):
f = quad()
return f[-1]
|
243 ms
#3
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution:
def minDistance(self, houses: List[int], k: int) -> int:
def quad(mid):
def w(a,b):
return mid+g[a]+p[b]-p[(a+b)//2]-(p[(a+b+1)//2]-p[a])
g = [0]+[inf]*n
h = [0]*(n+1)
Q = deque([[0,1,n]])
for j in range(1,n+1):
while Q and Q[0][2]<j:
Q.popleft()
g[j] = w(Q[0][0],j)
h[j] = h[Q[0][0]]+1
while Q and w(j,Q[-1][1])<w(Q[-1][0],Q[-1][1]):
Q.pop()
if not Q:
Q.append([j,j+1,n])
else:
a = bisect_left(range(Q[-1][2]+1),True,j,key=lambda a:w(j,a)<w(Q[-1][0],a))
Q[-1][2] = a-1
if a<=n:
Q.append([j,a,n])
return g,h
A = sorted(houses)
n = len(A)
p = [0]+list(accumulate(A))
l,r = 0,p[-1]
while l<=r:
mid = (l+r)//2
g,h = quad(mid)
if h[-1]<=k:
res = g[-1]-mid*k
if h[-1]==k:
break
r = mid-1
else:
l = mid+1
return res
|
95 ms

