1457:二叉树中的伪回文路径(1405 分)
目录
题目
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。
请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。
示例 1:
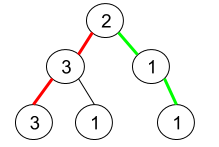
输入:root = [2,3,1,3,1,null,1] 输出:2 解释:上图为给定的二叉树。总共有 3 条从根到叶子的路径:红色路径 [2,3,3] ,绿色路径 [2,1,1] 和路径 [2,3,1] 。 在这些路径中,只有红色和绿色的路径是伪回文路径,因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ,绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
示例 2:
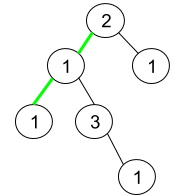
输入:root = [2,1,1,1,3,null,null,null,null,null,1] 输出:1 解释:上图为给定二叉树。总共有 3 条从根到叶子的路径:绿色路径 [2,1,1] ,路径 [2,1,3,1] 和路径 [2,1] 。 这些路径中只有绿色路径是伪回文路径,因为 [2,1,1] 存在回文排列 [1,2,1] 。
示例 3:
输入:root = [9] 输出:1
提示:
- 给定二叉树的节点数目在范围
[1, 105]内 1 <= Node.val <= 9
分析
一个序列最多有 1 个值出现奇数次,就可以排列成回文。
因此遍历时存储每个值出现次数即可。进一步的,因为只关心次数的奇偶,所以可以用二进制位来表示,压缩成一个数。
解答
|
|
832 ms