力扣第 22 场双周赛第 4 题
题目
给你一个披萨,它由 3n 块不同大小的部分组成,现在你和你的朋友们需要按照如下规则来分披萨:
- 你挑选 任意 一块披萨。
- Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
- Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
- 重复上述过程直到没有披萨剩下。
每一块披萨的大小按顺时针方向由循环数组 slices 表示。
请你返回你可以获得的披萨大小总和的最大值。
示例 1:
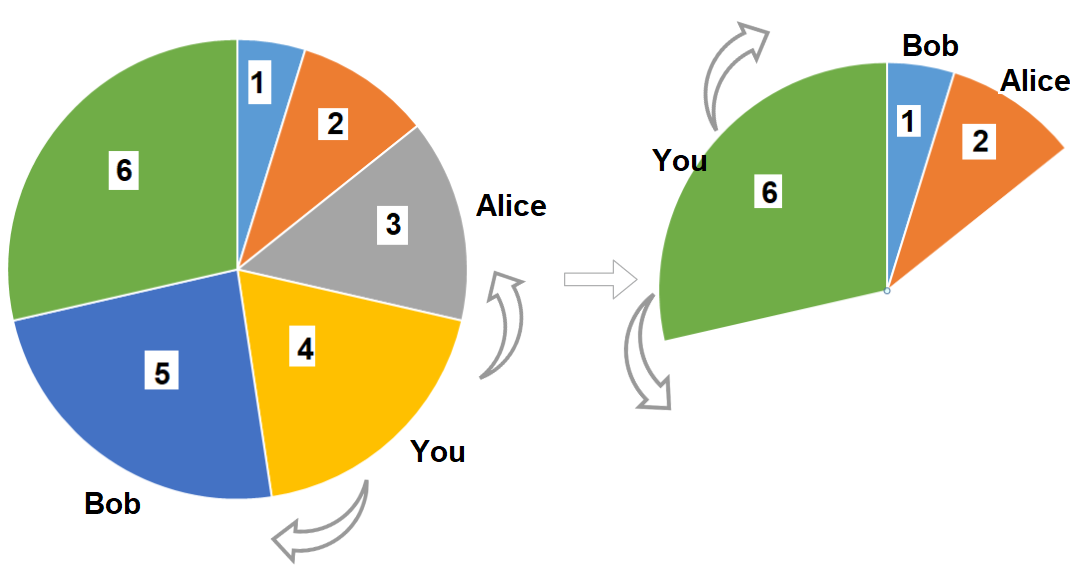
输入:slices = [1,2,3,4,5,6]
输出:10
解释:选择大小为 4 的披萨,Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨,Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。
示例 2:
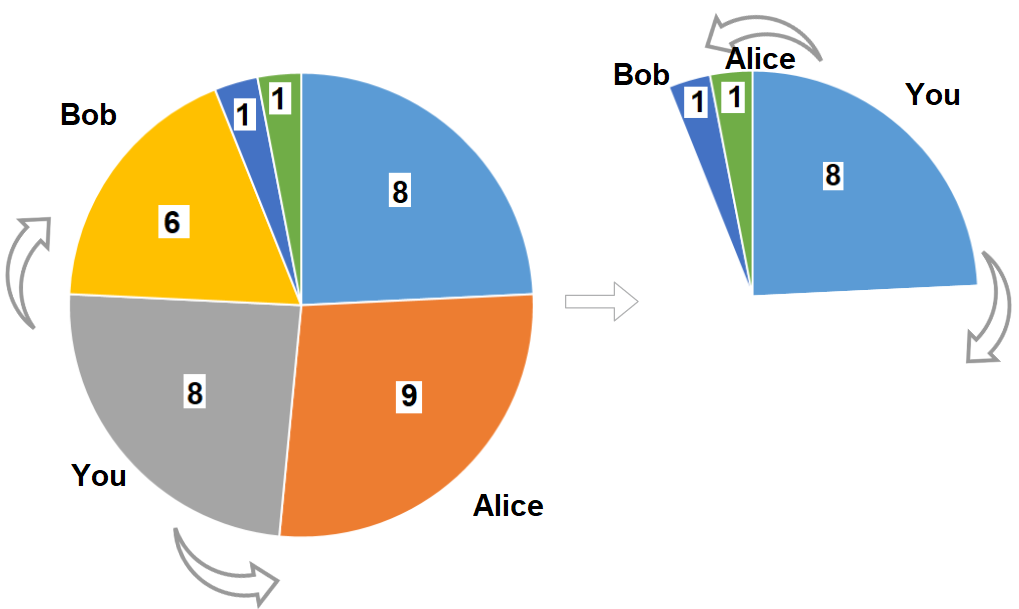
输入:slices = [8,9,8,6,1,1]
输出:16
解释:两轮都选大小为 8 的披萨。如果你选择大小为 9 的披萨,你的朋友们就会选择大小为 8 的披萨,这种情况下你的总和不是最大的。
提示:
1 <= slices.length <= 500slices.length % 3 == 01 <= slices[i] <= 1000
分析
#1 贪心+dp
- 如果直接考虑先取一块并递归的话,由于是环状,首尾重新相连,复杂度非常高
- 数据中试验后,直觉上来说,只要 k 块披萨不相邻,总能取到。再证明一下:
- 将要取的 k 块披萨和右侧(即顺时针的下一块)绑定,得到 k 个双块披萨和 k 个单块披萨
- 由于是环状,必然有个双块披萨的左侧是单块披萨,先选取它,去掉这三块披萨
- 依此类推,即可选到想要的 k 块披萨
- 问题简化为取 k 个不相邻的元素,使和最大
- 可以按选不选末尾元素递推了,还可以用滚动数组优化
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution:
def maxSizeSlices(self, slices: List[int]) -> int:
n = len(slices)
res,k = 0,n//3
for A in [slices[:-1],slices[1:]]:
f = [0]*n
for _ in range(k):
g = [0]*n
for i in range(1,n):
g[i] = max(g[i-1],A[i-1]+f[max(0,i-2)])
f = g
res = max(res,f[-1])
return res
|
179 ms
#2 反悔贪心
1
2
3
4
5
6
7
8
9
10
11
|
class Solution:
def maxSizeSlices(self, slices: List[int]) -> int:
res, A = 0, slices
for _ in range(len(A)//3):
i = A.index(max(A))
res += A[i]
a,b = sorted([(i-1)%len(A),(i+1)%len(A)])
A[i] = A[a]+A[b]-A[i]
A.pop(b)
A.pop(a)
return res
|
3 ms
#3 堆+双向链表
- 也可以用堆+双向链表优化删除过程
- python 可以用数组 L 和 R 模拟双向链表
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution:
def maxSizeSlices(self, slices: List[int]) -> int:
A = slices
n = len(A)
L = [n-1]+list(range(n-1))
R = list(range(1,n))+[0]
res = 0
pq = sorted((-x,i) for i,x in enumerate(A))
vis = [0]*n
for _ in range(n//3):
while vis[pq[0][1]]:
heappop(pq)
x,i = heappop(pq)
res -= x
a,b = L[i],R[i]
A[i] = A[a]+A[b]+x
heappush(pq,(-A[i],i))
vis[a] = vis[b] = 1
l,r = L[a],R[b]
L[i],R[i] = l,r
R[l] = L[r] = i
return res
|
3 ms
*附加
还可以用 wqs 二分
- 注意上述的贪心过程中每轮选的最大的 A[i],故添加的新值 A[i-1]+A[i+1]-A[i]<=A[i],因此每轮选的值是递减的
- 因此符合 wqs 二分的条件
- wqs 二分详见 一种基于 wqs 二分的优秀做法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution:
def maxSizeSlices(self, slices: List[int]) -> int:
n = len(slices)
res,k = 0,n//3
for A in [slices[1:],slices[:-1]]:
s = 0
l, r = 0, max(A)
while l<=r:
mid = (l+r)//2
a,aw,b,bw = 0,0,0,0
for x in A:
(a,aw),(b,bw) = (b,bw),(x-mid+a,aw+1) if x-mid+a>b else (b,bw)
if bw<=k:
s = b+mid*k
r = mid-1
else:
l = mid+1
res = max(res,s)
return res
|
11 ms

