力扣第 175 场周赛第 4 题
题目
给你一个 m * n 的矩阵 seats 表示教室中的座位分布。如果座位是坏的(不可用),就用 '#' 表示;否则,用 '.' 表示。
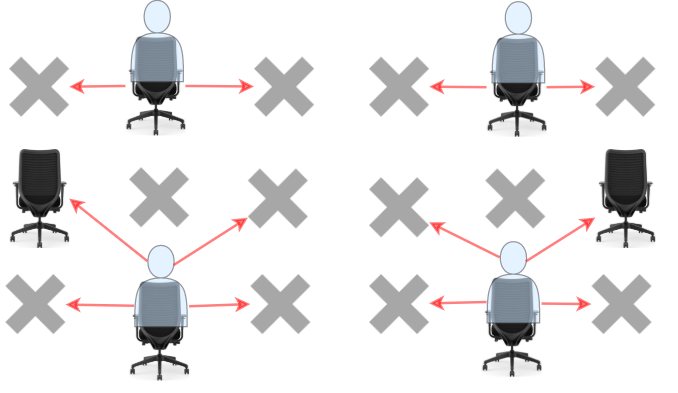
学生可以看到左侧、右侧、左上、右上这四个方向上紧邻他的学生的答卷,但是看不到直接坐在他前面或者后面的学生的答卷。请你计算并返回该考场可以容纳的同时参加考试且无法作弊的 最大 学生人数。
学生必须坐在状况良好的座位上。
示例 1:
输入:seats = [["#",".","#","#",".","#"],
[".","#","#","#","#","."],
["#",".","#","#",".","#"]]
输出:4
解释:教师可以让 4 个学生坐在可用的座位上,这样他们就无法在考试中作弊。
示例 2:
输入:seats = [[".","#"],
["#","#"],
["#","."],
["#","#"],
[".","#"]]
输出:3
解释:让所有学生坐在可用的座位上。
示例 3:
输入:seats = [["#",".",".",".","#"],
[".","#",".","#","."],
[".",".","#",".","."],
[".","#",".","#","."],
["#",".",".",".","#"]]
输出:10
解释:让学生坐在第 1、3 和 5 列的可用座位上。
提示:
seats 只包含字符 '.' 和'#'m == seats.lengthn == seats[i].length1 <= m <= 81 <= n <= 8
分析
#1
按每一行选哪些学生,即可递推
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
```python
class Solution:
def maxStudents(self, seats: List[List[str]]) -> int:
m,n = len(seats),len(seats[0])
f = {0:0}
for row in seats:
row = sum(1<<i for i,x in enumerate(row) if x=='#')
g = defaultdict(int)
for v in range(1<<n):
if not (v&(v>>1) or v&row):
w2 = v.bit_count()
for u,w in f.items():
if not ((u>>1)&v or (u<<1)&v):
g[v] = max(g[v],w+w2)
f = g
return max(f.values())
|
12 ms
#2
还可以按每个位置递推,即是轮廓线 dp,注意需要维护 n+1 长的轮廓
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def maxStudents(self, seats: List[List[str]]) -> int:
m,n = len(seats),len(seats[0])
mask = (1<<(n+1))-1
f = {0:0}
for row in seats:
for j,x in enumerate(row):
g = defaultdict(int)
for u,w in f.items():
if j==0:
u = (u<<1)&mask
v = (u|1<<j)^1<<j
g[v] = max(g[v],w)
if x=='.' and not any(0<=k<=n and u&1<<k for k in [j-1,j,j+2]):
v = u|1<<j
g[v] = max(g[v],w+1)
f = g
return max(f.values())
|
27 ms
#3
还可以看作 图匹配 问题
- 由于限制只在相邻的列之间,把座位看作点,限制看作边,这即是一个二分图
- 那么题目所求的即是最大独立集,即是 n-最大匹配
- 二分图最大匹配可以用匈牙利算法,也可以转网络流模型用 dinic 算法
- 本题数据很小,采用匈牙利算法
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
def hgr(g): # g 是二分图中每个 x 对应的 y 列表
def find(x):
for y in g[x]:
if y not in vis:
vis.add(y)
if y not in d or find(d[y]):
d[y]=x
return True
return False
res,vis,d = 0,set(),{}
for x in g:
res += find(x)
vis.clear()
return res
class Solution:
def maxStudents(self, seats: List[List[str]]) -> int:
m,n = len(seats),len(seats[0])
res = 0
g = defaultdict(list)
for i,j in product(range(m),range(n)):
if seats[i][j]=='.':
res += 1
for x,y in [(i,j-1),(i-1,j-1),(i-1,j+1)]:
if 0<=x<m and 0<=y<n and seats[x][y]=='.':
if j&1:
g[i*n+j].append(x*n+y)
else:
g[x*n+y].append(i*n+j)
return res-hgr(g)
|
0 ms
