1326：灌溉花园的最少水龙头数目（1885 分）

力扣第 172 场周赛第 4 题

题目

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

示例 1：

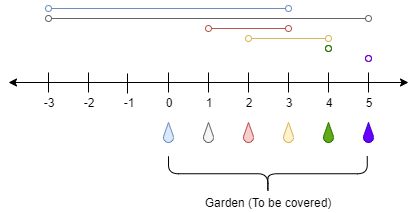
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。

示例 2：

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

提示：

• 1 <= n <= 104
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

分析

• 本质上是求用最少的区间覆盖的问题，类似于 0045
• 递推第 i 步能覆盖的新区间即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class Solution:
    def minTaps(self, n: int, ranges: List[int]) -> int:
        A = list(range(n+1))
        for i,x in enumerate(ranges):
            j = max(0,i-x)
            A[j] = max(A[j],i+x)
        res,l,r = 0,0,0
        while l<=r<n:
            l,r = r+1,max(A[i] for i in range(l,r+1))
            res += 1
        return res if r>=n else -1

19 ms