1235：规划兼职工作（2022 分）

力扣第 159 场周赛第 4 题

题目

你打算利用空闲时间来做兼职工作赚些零花钱。

这里有 n 份兼职工作，每份工作预计从 startTime[i] 开始到 endTime[i] 结束，报酬为 profit[i]。

给你一份兼职工作表，包含开始时间 startTime，结束时间 endTime 和预计报酬 profit 三个数组，请你计算并返回可以获得的最大报酬。

注意，时间上出现重叠的 2 份工作不能同时进行。

如果你选择的工作在时间 X 结束，那么你可以立刻进行在时间 X 开始的下一份工作。

示例 1：

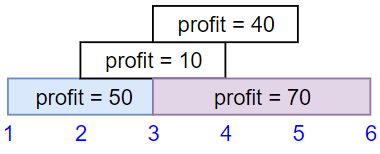
输入：startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出：120
解释：
我们选出第 1 份和第 4 份工作，
时间范围是 [1-3]+[3-6]，共获得报酬 120 = 50 + 70。

示例 2：

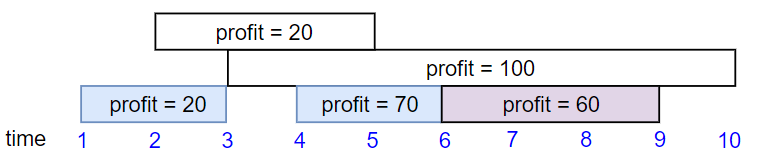
输入：startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出：150
解释：
我们选择第 1，4，5 份工作。
共获得报酬 150 = 20 + 70 + 60。

示例 3：

输入：startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出：6

提示：

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
• 1 <= startTime[i] < endTime[i] <= 10^9
• 1 <= profit[i] <= 10^4

相似问题：

• 2008：出租车的最大盈利（1871 分）
• 2054：两个最好的不重叠活动（1883 分）

分析

• 若选了第一个工作，那么接下来从开始时间 >= endTime[0] 的工作中选
• 因此先把工作按开始时间排序，二分查找到第一个满足的 j，即转为递归子问题

解答

1
2
3
4
5
6
7
8
9

class Solution:
    def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
        A = sorted(zip(startTime,endTime,profit))
        n = len(A)
        f = [0]*(n+1)
        for i in range(n-1,-1,-1):
            j = bisect_left(A,(A[i][1],))
            f[i] = max(f[i+1],f[j]+A[i][2])
        return f[0]

178 ms