1206：设计跳表（★★）

Ian

2019-09-25 约 765 字预计阅读 2 分钟次阅读

力扣第 1206 题

题目

不使用任何库函数，设计一个跳表。

跳表是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：

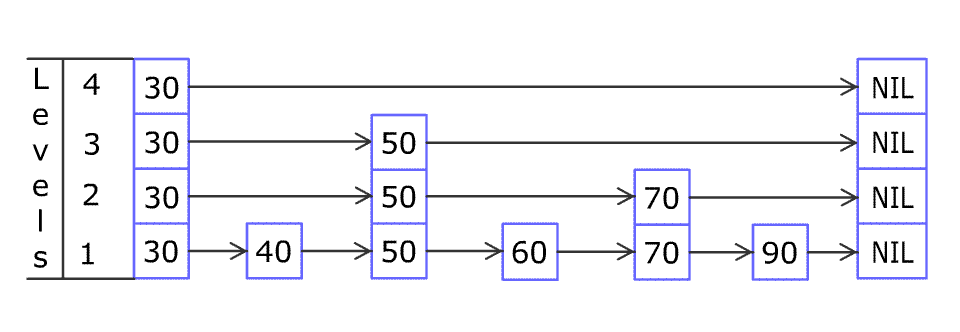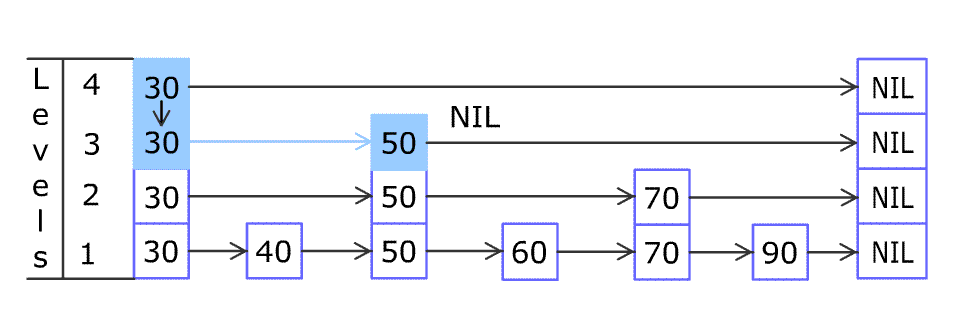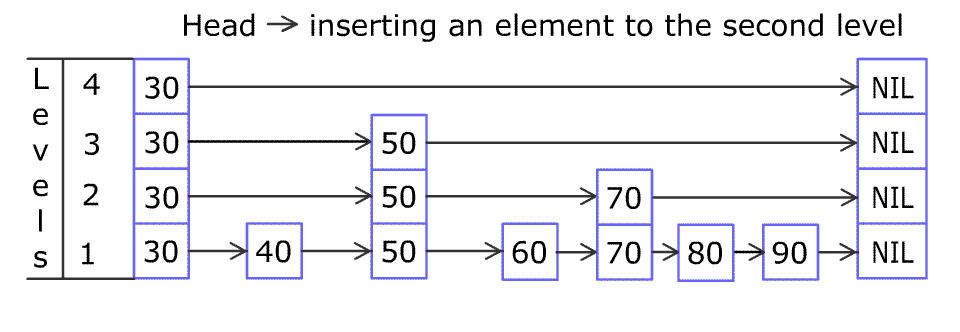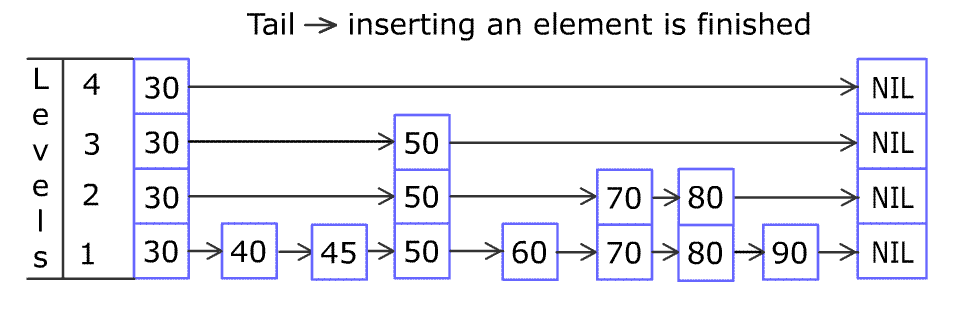
跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

了解更多 : https://oi-wiki.org/ds/skiplist/

在本题中，你的设计应该要包含这些函数：

bool search(int target) : 返回target是否存在于跳表中。
void add(int num): 插入一个元素到跳表。
bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

示例 1:

输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除

提示:

0 <= num, target <= 2 * 10⁴
调用search, add, erase操作次数不大于 5 * 10⁴

相似问题：

分析

跳表教程

为了方便，可以将叠在一起的看成是一个节点。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


class Node:

    def __init__(self, val, nxt=[]):
        self.val = val
        self.nxt = nxt

class Skiplist:

    def __init__(self):
        self.tail = Node(float('inf'))
        self.head = Node(-float('inf'), [self.tail])
        self.H = 0 

    def search(self, target: int) -> bool:
        cur = self.head
        for h in range(self.H, -1, -1):
            while cur.nxt[h].val <= target:
                cur = cur.nxt[h]
        return cur.val == target

    def add(self, num: int) -> None:
        cur, path = self.head, [None] * (self.H+1)
        for h in range(self.H, -1, -1):
            while cur.nxt[h].val <= num:
                cur = cur.nxt[h]
            path[h] = cur
        node = Node(num, [path[0].nxt[0]])
        path[0].nxt[0] = node
        h = 1
        while random.random() > 0.5:
            if h > self.H:
                self.head.nxt.append(node)
                node.nxt.append(self.tail)
                self.H += 1
            else:
                node.nxt.append(path[h].nxt[h])
                path[h].nxt[h] = node
            h += 1

    def erase(self, num: int) -> bool:
        cur, flag = self.head, False
        for h in range(self.H, -1, -1):
            while cur.nxt[h].val < num:
                cur = cur.nxt[h]
            if cur.nxt[h].val == num:
                flag = True
                cur.nxt[h] = cur.nxt[h].nxt[h]
        return flag

232 ms

目录

1206：设计跳表（★★）

题目

分析

解答