1203：项目管理（2418 分）

2019-09-22 约 757 字预计阅读 2 分钟次阅读

力扣第 155 场周赛第 4 题

题目

有 n 个项目，每个项目或者不属于任何小组，或者属于 m 个小组之一。group[i] 表示第 i 个项目所属的小组，如果第 i 个项目不属于任何小组，则 group[i] 等于 -1。项目和小组都是从零开始编号的。可能存在小组不负责任何项目，即没有任何项目属于这个小组。

请你帮忙按要求安排这些项目的进度，并返回排序后的项目列表：

同一小组的项目，排序后在列表中彼此相邻。
项目之间存在一定的依赖关系，我们用一个列表 beforeItems 来表示，其中 beforeItems[i] 表示在进行第 i 个项目前（位于第 i 个项目左侧）应该完成的所有项目。

如果存在多个解决方案，只需要返回其中任意一个即可。如果没有合适的解决方案，就请返回一个 空列表 。

示例 1：

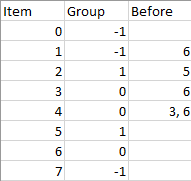
输入：n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
输出：[6,3,4,1,5,2,0,7]

示例 2：

输入：n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
输出：[]
解释：与示例 1 大致相同，但是在排序后的列表中，4 必须放在 6 的前面。

提示：

1 <= m <= n <= 3 * 10⁴
group.length == beforeItems.length == n
-1 <= group[i] <= m - 1
0 <= beforeItems[i].length <= n - 1
0 <= beforeItems[i][j] <= n - 1
i != beforeItems[i][j]
beforeItems[i] 不含重复元素

分析

将依赖关系看作有向边，显然是一个拓扑排序问题
- 同一小组的必须相邻，将小组看作顶点，小组间要满足拓扑顺序
- 小组排好后，每个小组内部也要满足拓扑顺序
具体实现时
- 将不属于任何小组的项目分给一个单独的虚拟小组，方便统一解决
- 将小组看作顶点，建图，并将组内边分给对应的小组
- 先对小组顶点拓扑排序，再根据小组内的点和边拓扑排序即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


class Solution:
    def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:
        def topo(V, E):
            g, deg = defaultdict(list), defaultdict(int)
            for u,v in E:
                g[u].append(v)
                deg[v] += 1
            res, Q = [], deque(u for u in V if deg[u]==0)
            while Q:
                u = Q.popleft()
                res.append(u)
                for v in g[u]:
                    deg[v] -= 1
                    if deg[v] == 0:
                        Q.append(v)
            return res if len(res)==len(V) else []

        M = m
        for i in range(n):
            if group[i] == -1:
                group[i] = M
                M += 1
        outV, inV = set(group), defaultdict(list)
        for i in range(n):
            inV[group[i]].append(i)
        outE, inE = [], defaultdict(list)
        for v in range(n):
            for u in beforeItems[v]:
                if group[u] == group[v]:
                    inE[group[u]].append([u, v])
                else:
                    outE.append([group[u], group[v]])
        res = [v for g in topo(outV, outE) for v in topo(inV[g], inE[g])]
        return res if len(res)==n else []

135 ms

目录

1203：项目管理（2418 分）

题目

分析

解答