1168：水资源分配优化（★★）

力扣第 7 场双周赛第 4 题

题目

村里面一共有 n 栋房子。我们希望通过建造水井和铺设管道来为所有房子供水。

对于每个房子 i，我们有两种可选的供水方案：一种是直接在房子内建造水井，成本为 wells[i - 1] （注意 -1 ，因为 索引从0开始 ）；另一种是从另一口井铺设管道引水，数组 pipes 给出了在房子间铺设管道的成本，其中每个 pipes[j] = [house1j, house2j, costj] 代表用管道将 house1j 和 house2j连接在一起的成本。连接是双向的。

请返回 为所有房子都供水的最低总成本 。

示例 1：

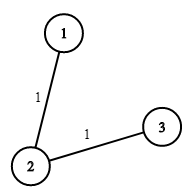
输入：n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
输出：3
解释： 
上图展示了铺设管道连接房屋的成本。
最好的策略是在第一个房子里建造水井（成本为 1），然后将其他房子铺设管道连起来（成本为 2），所以总成本为 3。

示例 2：

输入：n = 2, wells = [1,1], pipes = [[1,2,1]]
输出：2
解释：我们可以用以下三种方法中的一种来提供低成本的水:
选项1:
在1号房子里面建一口井，成本为1
在房子2内建造井，成本为1
总成本是2。
选项2:
在1号房子里面建一口井，成本为1
-花费1连接房子2和房子1。
总成本是2。
选项3:
在房子2内建造井，成本为1
-花费1连接房子1和房子2。
总成本是2。
注意，我们可以用cost 1或cost 2连接房子1和房子2，但我们总是选择最便宜的选项。

提示：

• 2 <= n <= 104
• wells.length == n
• 0 <= wells[i] <= 105
• 1 <= pipes.length <= 104
• pipes[j].length == 3
• 1 <= house1j, house2j <= n
• 0 <= costj <= 105
• house1j != house2j

分析

• 设一个虚拟节点 0 代表水，房子造井看作是铺设了到节点 0 的管道
• 转为求最小生成树问题，用并查集即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution:
    def minCostToSupplyWater(self, n: int, wells: List[int], pipes: List[List[int]]) -> int:
        def find(x):
            if f[x] != x:
                f[x] = find(f[x])
            return f[x]

        pipes.extend([0, i+1, w] for i, w in enumerate(wells))
        res, f = 0, list(range(n+1))
        for x, y, w in sorted(pipes, key=lambda x: x[-1]):
            fx, fy = find(x), find(y)
            if fx != fy:
                f[fx] = fy
                res += w
        return res

140 ms