1130:叶值的最小代价生成树(1919 分)
目录
题目
给你一个正整数数组 arr,考虑所有满足以下条件的二叉树:
- 每个节点都有
0个或是2个子节点。 - 数组
arr中的值与树的中序遍历中每个叶节点的值一一对应。 - 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中,返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。
如果一个节点有 0 个子节点,那么该节点为叶节点。
示例 1:
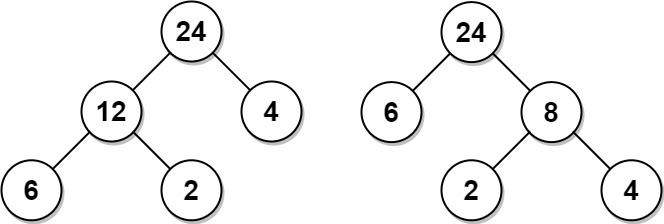
输入:arr = [6,2,4] 输出:32 解释:有两种可能的树,第一种的非叶节点的总和为 36 ,第二种非叶节点的总和为 32 。
示例 2:
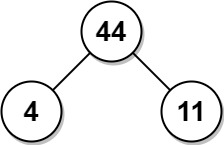
输入:arr = [4,11] 输出:44
提示:
2 <= arr.length <= 401 <= arr[i] <= 15- 答案保证是一个 32 位带符号整数,即小于
231。
分析
#1
数据规模很小,考虑直接递归。满足条件的二叉树必然是以 arr[:i] 为左子树,arr[i:] 为右子树。 并且如果 len(arr) > 1,左子树和右子树都至少有一个节点。
因此遍历位置 0<i<len(arr),根节点的值为 max(arr[:i]) * max(arr[i:]),剩下的即为递归子问题。
|
|
296 ms
#2
本题有个很巧妙的单调栈解法。
本题可以等价于一个数组问题:每一轮从 arr 中选择两个相邻的数,得到一个乘积,并删除较小的那个数,直到数组长度小于 2,求最小的乘积之和。
如果存在 arr[i-1] >= arr[i] <= arr[i+1],最终 arr[i] 必然是要被删除的(或者等价于 arr[i] 被删除)。 假设最优方略是在删除了 arr[i-1] 或 arr[i+1] 之后才删除的 arr[i],arr[i] 相邻的两个数会相等或更大。那么改成先删除 arr[i],不会比最优方案差。
因此遇到 arr[i-1] >= arr[i] <= arr[i+1] 时,即可先将 arr[i] 删除,这正符合单调栈的过程。
注意最后栈中可能还剩余元素,显然应该反向删除。
解答
|
|
48 ms