0968：监控二叉树（2124 分）

力扣第 117 场周赛第 4 题

题目

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

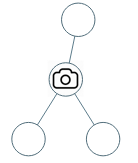
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

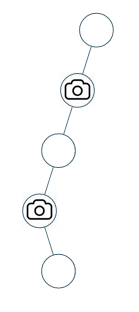
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

1. 给定树的节点数的范围是 [1, 1000]。
2. 每个节点的值都是 0。

相似问题：

• 0979：在二叉树中分配硬币（1709 分）
• 2378：选择边来最大化树的得分

分析

• 按根节点装不装讨论
  • 根节点装，转为求 “子树根节点不用监视情况下的最小数量”
  • 根节点不装，子树中至少有一个要装在根节点，转为求 “根节点装的情况下的最小数量”
• 因此令 dfs 同时返回 “所有情况的最小数量”、“根节点装时的最小数量”、“不用监视根节点时的最小数量”，进行递推
  • 假设左子树返回的 l1,l2,l3，右子树返回的 r1,r2,r3
  • 根节点装时，显然就是 1+l3+r3
  • 根节点不装时，要么左子树根节点装，为 l2+r1，要么右子树根节点装，为 l1+r2
  • 不用监视根节点时，要么根节点装，为 1+l3+r3，要么根节点不装，为 l1+r1

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution:
    def minCameraCover(self, root: Optional[TreeNode]) -> int:
        def dfs(u):
            if not u:
                return 0,inf,0
            l1,l2,l3 = dfs(u.left)
            r1,r2,r3 = dfs(u.right)
            a = 1+l3+r3
            return min(a,l2+r1,l1+r2),a,min(a,l1+r1)
        return dfs(root)[0]

7 ms