0913：猫和老鼠（2566 分）

Ian

2018-09-30 约 1060 字预计阅读 3 分钟次阅读

力扣第 104 场周赛第 4 题

题目

两位玩家分别扮演猫和老鼠，在一张无向图上进行游戏，两人轮流行动。

图的形式是：graph[a] 是一个列表，由满足 ab 是图中的一条边的所有节点 b 组成。

老鼠从节点 1 开始，第一个出发；猫从节点 2 开始，第二个出发。在节点 0 处有一个洞。

在每个玩家的行动中，他们必须沿着图中与所在当前位置连通的一条边移动。例如，如果老鼠在节点 1 ，那么它必须移动到 graph[1] 中的任一节点。

此外，猫无法移动到洞中（节点 0）。

然后，游戏在出现以下三种情形之一时结束：

如果猫和老鼠出现在同一个节点，猫获胜。
如果老鼠到达洞中，老鼠获胜。
如果某一位置重复出现（即，玩家的位置和移动顺序都与上一次行动相同），游戏平局。

给你一张图 graph ，并假设两位玩家都都以最佳状态参与游戏：

如果老鼠获胜，则返回 1；
如果猫获胜，则返回 2；
如果平局，则返回 0 。

示例 1：

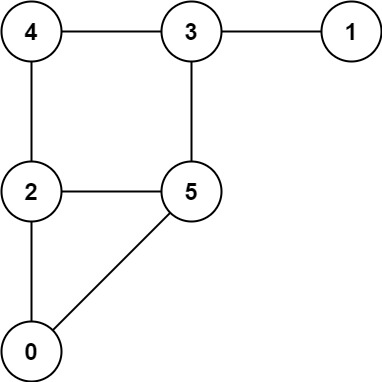
输入：graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
输出：0

示例 2：

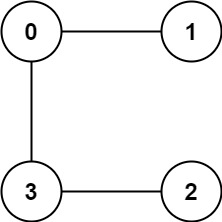
输入：graph = [[1,3],[0],[3],[0,2]]
输出：1

提示：

3 <= graph.length <= 50
1 <= graph[i].length < graph.length
0 <= graph[i][j] < graph.length
graph[i][j] != i
graph[i] 互不相同
猫和老鼠在游戏中总是可以移动

相似问题：

1728：猫和老鼠 II（2849 分）

分析

经典的博弈问题，直接递归的话状态数太多，更优且更通用的做法是从终态反推
- 终态有两种
  - 猫的必胜态：猫和老鼠在同一个节点
  - 鼠的必胜态：老鼠在节点 0
- 考虑与终态相邻的状态
  - 对于轮到猫走的状态
    - 情况一：假如能转移到猫的必胜态，该状态便也是猫的必胜态
    - 情况二：假如能转移到的状态都是鼠的必胜态，该状态便也是鼠的必胜态
    - 否则，状态待定
  - 对于轮到鼠走的状态也同理
- 把确定的状态转为终态，继续一步步反推，直到所有剩下待定的状态，便都是平局状态
这个过程非常类似拓扑排序，只是判断入队的条件复杂一些
- 令状态 st=<i,j,1>或<i,j,2>，分别代表鼠在节点 i，猫在节点 j（注意 j!=0），轮到鼠/猫走
- 令 f[st]=1或2，分别代表状态 st 是鼠/猫的必胜态
- 针对状态 st 建图并统计出度，将终态入队
  - 注意建图是反向转移，出度是统计的正向转移
- 出队终态 u，遍历相邻的状态 v
  - 若 f[u]=v[-1]，对应上面分析的情况一，f[v]=f[u]
  - 否则，v 的出度减一，若出度为 0，对应上面的情况二，f[v]=f[u]
  - 两种情况的 v 都入队
- 循环直到状态 <1,2,1> 入队，或队空，返回平局态 0

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


class Solution:
    def catMouseGame(self, graph: List[List[int]]) -> int:
        n = len(graph)
        g, deg = {}, {}
        for i, j in product(range(n), range(1,n)):
            g[(i,j,1)] = [(i,y,2) for y in graph[j] if y!=0]
            g[(i,j,2)] = [(x,j,1) for x in graph[i]]
            deg[(i,j,1)] = len(graph[i])
            deg[(i,j,2)] = sum(y!=0 for y in graph[j])
        f = {}
        for j in range(1,n):
            f[(j,j,1)] = f[(j,j,2)] = 2
            f[(0,j,1)] = f[(0,j,2)] = 1
        Q = deque(f)
        while Q:
            u = Q.popleft()
            if u==(1,2,1):
                return f[u]
            for v in g[u]:
                if v in f:
                    continue
                if v[-1]==f[u]:
                    f[v] = f[u]
                    Q.append(v)
                else:
                    deg[v] -= 1
                    if deg[v] == 0:
                        f[v] = f[u]
                        Q.append(v)
        return 0

541 ms

目录

0913：猫和老鼠（2566 分）

题目

分析

解答