力扣第 92 场周赛第 4 题
题目
给定一个二维网格 grid ,其中:
- '.' 代表一个空房间
- '#' 代表一堵墙
- '@' 是起点
- 小写字母代表钥匙
- 大写字母代表锁
我们从起点开始出发,一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走,也无法穿过一堵墙。如果途经一个钥匙,我们就把它捡起来。除非我们手里有对应的钥匙,否则无法通过锁。
假设 k 为 钥匙/锁 的个数,且满足 1 <= k <= 6,字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之,每个锁有唯一对应的钥匙,每个钥匙也有唯一对应的锁。另外,代表钥匙和锁的字母互为大小写并按字母顺序排列。
返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙,返回 -1 。
示例 1:
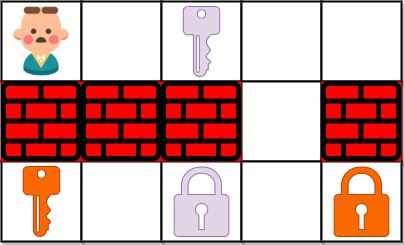
输入:grid = ["@.a..","###.#","b.A.B"]
输出:8
解释:目标是获得所有钥匙,而不是打开所有锁。
示例 2:
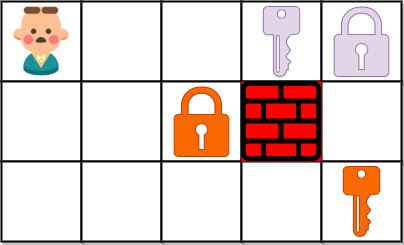
输入:grid = ["@..aA","..B#.","....b"]
输出:6
示例 3:

输入: grid = ["@Aa"]
输出: -1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j] 只含有 '.', '#', '@', 'a'-'f' 以及 'A'-'F'- 钥匙的数目范围是
[1, 6]
- 每个钥匙都对应一个 不同 的字母
- 每个钥匙正好打开一个对应的锁
分析
#1
将状态 <位置,钥匙集合> 看作顶点,就是典型的 bfs 问题,遍历即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution:
def shortestPathAllKeys(self, grid: List[str]) -> int:
m, n = len(grid), len(grid[0])
d = {grid[i][j]:(i,j) for i in range(m) for j in range(n)}
si, sj = d['@']
tg = sum(1<<i for i in range(6) if chr(ord('a')+i) in d)
Q, vis = deque([(0,si,sj,0)]), {(si,sj,0)}
while Q:
w,i,j,st = Q.popleft()
if st==tg:
return w
for x,y in [(i+1,j),(i-1,j),(i,j+1),(i,j-1)]:
if 0<=x<m and 0<=y<n and grid[x][y]!='#':
c = grid[x][y]
if c in 'ABCDEF' and not st&1<<(ord(c)-ord('A')):
continue
st2 = st|1<<(ord(c)-ord('a')) if c in 'abcdef' else st
if (x,y,st2) not in vis:
Q.append((w+1,x,y,st2))
vis.add((x,y,st2))
return -1
|
183 ms
#2
- 注意到只有钥匙和锁的位置是重要的,它们之间的距离是固定的
- 因此建立新图,只包含起点和钥匙、锁的位置,预处理它们之间的距离
- 仍然以状态 <位置,钥匙集合> 作为顶点,变为典型的最短路问题,用 dijkstra 即可
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
class Solution:
def shortestPathAllKeys(self, grid: List[str]) -> int:
def bfs(i,j):
Q = deque([(0,i,j)])
d = defaultdict(lambda:inf)
d[(i,j)] = 0
while Q:
w,i,j = Q.popleft()
for x,y in [(i+1,j),(i-1,j),(i,j+1),(i,j-1)]:
if 0<=x<m and 0<=y<n and grid[x][y]!='#' and (x,y) not in d:
d[(x,y)] = w+1
if grid[x][y] not in 'ABCDEF':
Q.append((w+1,x,y))
return [d[(x,y)] for x,y in A]
m,n = len(grid),len(grid[0])
g = defaultdict(list)
for i,j in product(range(m),range(n)):
g[grid[i][j]].append((i,j))
tg = sum(1<<i for i in range(6) if chr(ord('a')+i) in g)
A = [(i,j) for c in '@abcdefABCDEF' for i,j in g[c]]
f = [bfs(i,j) for i,j in A]
pq = [(0,0,0)]
d = defaultdict(lambda:inf)
d[(0,0)] = 0
while pq:
w,u,st = heappop(pq)
if st==tg:
return w
if w>d[(u,st)]:
continue
for v,(i,j) in enumerate(A):
c = grid[i][j]
if c in 'ABCDEF' and not st&1<<(ord(c)-ord('A')):
continue
w2 = w+f[u][v]
st2 = st|1<<(ord(c)-ord('a')) if c in 'abcdef' else st
if w2<d[(v,st2)]:
d[(v,st2)]=w2
heappush(pq,(w2,v,st2))
return -1
|
71 ms


