力扣第 88 场周赛第 4 题
题目
给你一个轴对齐的二维数组 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标, (xi1, yi1) 是该矩形 左下角 的坐标, (xi2, yi2) 是该矩形 右上角 的坐标。
计算平面中所有 rectangles 所覆盖的 总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。
返回 总面积 。因为答案可能太大,返回 109 + 7 的 模 。
示例 1:
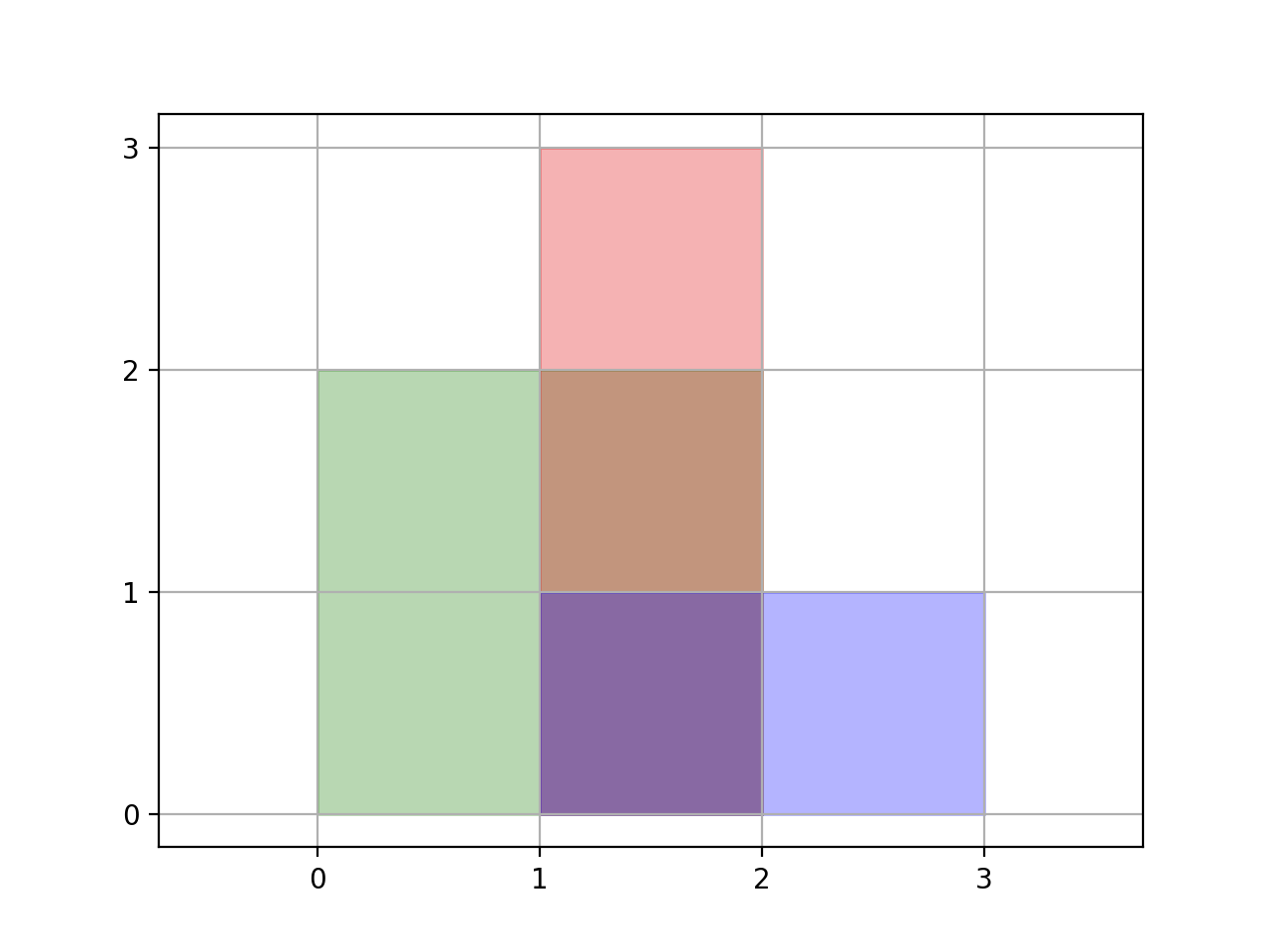
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出:6
解释:如图所示,三个矩形覆盖了总面积为 6 的区域。
从(1,1)到(2,2),绿色矩形和红色矩形重叠。
从(1,0)到(2,3),三个矩形都重叠。
示例 2:
输入:rectangles = [[0,0,1000000000,1000000000]]
输出:49
解释:答案是 1018 对 (109 + 7) 取模的结果, 即 49 。
提示:
1 <= rectangles.length <= 200rectanges[i].length = 40 <= xi1, yi1, xi2, yi2 <= 109
分析
#1
- 类似 0218,不过遍历坐标 x 时,要维护的不是高度集合,而是区间集合
- 每一轮根据当前横坐标 x2 、上一轮横坐标 x1,上一轮区间集合覆盖的长度 w,即可计算出 x1 到 x2 的面积
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
from sortedcontainers import SortedList
mod = 10**9+7
class Solution:
def rectangleArea(self, rectangles: List[List[int]]) -> int:
def cal(A):
res, end = 0, 0
for s, e in A:
res += max(end, e) - max(s, end)
end = max(end, e)
return res
d = defaultdict(list)
for x1,y1,x2,y2 in rectangles:
d[x1].append((1,y1,y2))
d[x2].append((0,y1,y2))
res = 0
H = SortedList()
for x1,x2 in pairwise(sorted(d)):
for flag,y1,y2 in d[x1]:
if flag:
H.add((y1,y2))
else:
H.remove((y1,y2))
res += cal(H)*(x2-x1)
res %= mod
return res
|
时间复杂度 O(N^2),15 ms
#2
- 还可以用线段树维护区间覆盖的长度 w
- 直接维护覆盖的长度不好处理,一种方法是维护 区间的最小值 t 和 t 对应的长度 sz
- 假如总区间的最小值 t>0,说明整个区间都被覆盖
- 否则 t=0,覆盖的长度为总区间长度 s - (t 对应的 sz)
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
class Seg:
def __init__(self,n):
self.L = n.bit_length()
self.N = N = 1<<self.L
self.t = [0]*N*2
self.f = [0]*N*2
self.sz = [0]*N*2
def apply(self,o,x):
self.t[o] += x
self.f[o] += x
def build(self,A):
for i in range(len(A)-1):
self.sz[self.N+i] = A[i+1]-A[i]
for o in range(self.N-1,0,-1):
self.pull(o)
def pull(self,o):
t,sz = self.t,self.sz
t[o] = min(t[o*2],t[o*2+1])
sz[o] = sz[o*2]*(t[o]==t[o*2])+sz[o*2+1]*(t[o]==t[o*2+1])
def push(self,o):
if self.f[o] != self.f[0]:
self.apply(o*2,self.f[o])
self.apply(o*2+1,self.f[o])
self.f[o] = self.f[0]
def modify(self,a,b,x):
a,b = a+self.N-1,b+self.N+1
for i in range(self.L,0,-1):
self.push(a>>i)
self.push(b>>i)
while a^b^1:
if not a&1: self.apply(a^1,x)
if b&1: self.apply(b^1,x)
a,b = a>>1,b>>1
self.pull(a)
self.pull(b)
while a>>1:
a >>= 1
self.pull(a)
mod = 10**9+7
class Solution:
def rectangleArea(self, rectangles: List[List[int]]) -> int:
d = defaultdict(list)
V = sorted({y for _,y1,_,y2 in rectangles for y in [y1,y2]})
mp = {y:i for i,y in enumerate(V)}
for x1,y1,x2,y2 in rectangles:
y1,y2 = mp[y1],mp[y2]-1
d[x1].append((y1,y2,1))
d[x2].append((y1,y2,-1))
res = 0
seg = Seg(len(V)-1)
seg.build(V)
for x1,x2 in pairwise(sorted(d)):
for y1,y2,flag in d[x1]:
seg.modify(y1,y2,flag)
w = V[-1]-V[0]-(seg.sz[1] if seg.t[1]==0 else 0)
res += w*(x2-x1)
res %= mod
return res
|
19 ms
