0847：访问所有节点的最短路径（2200 分）

Ian

2018-06-03 约 399 字预计阅读 1 分钟次阅读

力扣第 87 场周赛第 4 题

题目

存在一个由 n 个节点组成的无向连通图，图中的节点按从 0 到 n - 1 编号。

给你一个数组 graph 表示这个图。其中，graph[i] 是一个列表，由所有与节点 i 直接相连的节点组成。

返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。

示例 1：

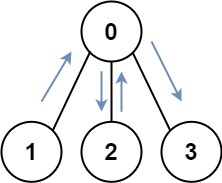
输入：graph = [[1,2,3],[0],[0],[0]]
输出：4
解释：一种可能的路径为 [1,0,2,0,3]

示例 2：

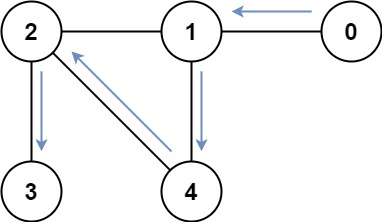
输入：graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
输出：4
解释：一种可能的路径为 [0,1,4,2,3]

提示：

n == graph.length
1 <= n <= 12
0 <= graph[i].length < n
graph[i] 不包含 i
如果 graph[a] 包含 b ，那么 graph[b] 也包含 a
输入的图总是连通图

相似问题：

3149：找出分数最低的排列（2641 分）

分析

典型的 bfs，维护状态 <节点 u, 访问过的节点集合 st> 即可
注意 set 类型不能作为哈希的键，将节点集合状态压缩成一个数即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)
        Q = deque([(0,i,1<<i) for i in range(n)])
        vis = {(i,1<<i) for i in range(n)}
        while Q:
            w,i,st = Q.popleft()
            if st==(1<<n)-1:
                return w
            for j in graph[i]:
                st2 = st|1<<j
                if (j,st2) not in vis:
                    vis.add((j,st2))
                    Q.append((w+1,j,st2))

131 ms

目录

0847：访问所有节点的最短路径（2200 分）

题目

分析

解答