0782：变为棋盘（2429 分）

力扣第 782 题

题目

一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动，你能任意交换两列或是两行的位置。

返回 将这个矩阵变为 “棋盘” 所需的最小移动次数 。如果不存在可行的变换，输出 -1。

“棋盘” 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。

示例 1:

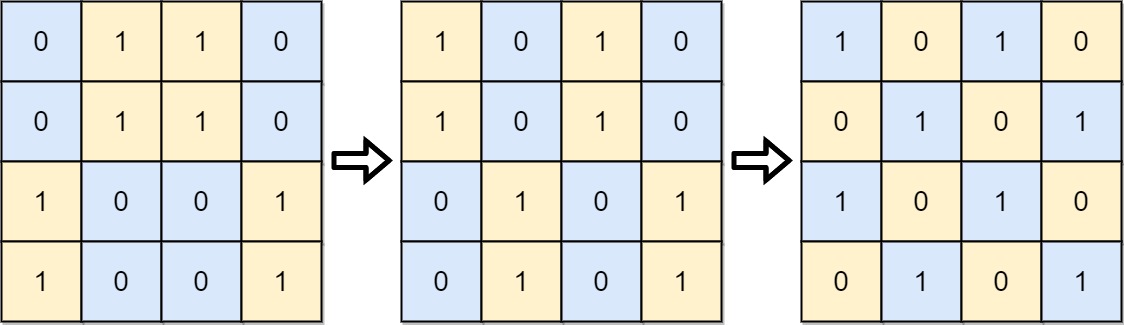
输入: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
输出: 2
解释:一种可行的变换方式如下，从左到右：
第一次移动交换了第一列和第二列。
第二次移动交换了第二行和第三行。

示例 2:

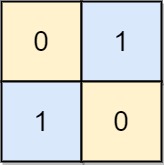
输入: board = [[0, 1], [1, 0]]
输出: 0
解释: 注意左上角的格值为0时也是合法的棋盘，也是合法的棋盘.

示例 3:

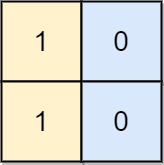
输入: board = [[1, 0], [1, 0]]
输出: -1
解释: 任意的变换都不能使这个输入变为合法的棋盘。

提示：

• n == board.length
• n == board[i].length
• 2 <= n <= 30
• board[i][j] 将只包含 0或 1

相似问题：

• 3189：得到一个和平棋盘的最少步骤

分析

• 首先看第一行，0 和 1 的个数之差不能超过 1
• 然后看第二行，和第一行相比，要么完全相等，要么完全相反
• 后面的行同理，列也同理
• 然后计算行交换的次数
  • 最后只可能得到两种结果：1 开始的交替序列，或 0 开始的交替序列
  • 对每个序列，计算不同的位置个数 diff，如果 diff 是偶数，交换次数即是 diff//2
• 列交换次数同理，最后相加即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution:
    def movesToChessboard(self, board: List[List[int]]) -> int:
        A = board[0]
        if abs(2*A.count(1)-len(A))>1:
            return -1
        A2 = [a^1 for a in A]
        if any(row not in [A,A2] for row in board):
            return -1
        B = [row[0] for row in board]
        if abs(2*B.count(1)-len(board))>1:
            return -1
        def cal(row,st):
            diff = sum(i&1^st^x for i,x in enumerate(row))
            return diff//2 if diff%2==0 else inf
        return min(cal(A,0),cal(A,1))+min(cal(B,0),cal(B,1))

3 ms