0750:角矩形的数量(★)
目录
题目
给定一个只包含 0 和 1 的 m x n 整数矩阵 grid ,返回 其中 「角矩形 」的数量 。
一个「角矩形」是由四个不同的在矩阵上的 1 形成的 轴对齐 的矩形。注意只有角的位置才需要为 1。
注意:4 个 1 的位置需要是不同的。
示例 1:
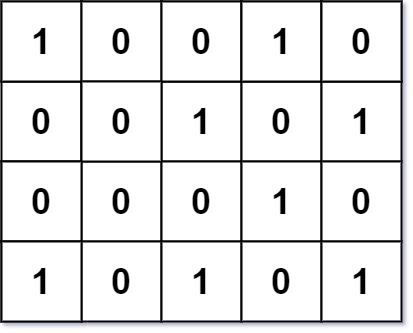
输入:grid = [[1,0,0,1,0],[0,0,1,0,1],[0,0,0,1,0],[1,0,1,0,1]] 输出:1 解释:只有一个角矩形,角的位置为 grid[1][2], grid[1][4], grid[3][2], grid[3][4]。
示例 2:

输入:grid = [[1,1,1],[1,1,1],[1,1,1]] 输出:9 解释:这里有 4 个 2x2 的矩形,4 个 2x3 和 3x2 的矩形和 1 个 3x3 的矩形。
示例 3:
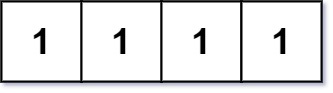
输入:grid = [[1,1,1,1]] 输出:0 解释:矩形必须有 4 个不同的角。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 200grid[i][j]不是0就是1- 网格中
1的个数在[1, 6000]范围内
分析
#1
先选定上下界 i 和 j,假如这两行中有 w 个位置同时为 1,则能组成 w*(w-1)//2 个矩形。
|
|
2876 ms
#2
由于只存在 0 和 1,可以将每一行转为二进制数,然后用位运算快速得到 w。
解答
|
|
148 ms