0685：冗余连接 II（★★）

Ian

2016-11-15 约 658 字预计阅读 2 分钟次阅读

力扣第 685 题

题目

在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。每个元素是一对 [u_i, v_i]，用以表示有向图中连接顶点 u_i 和顶点 v_i 的边，其中 u_i 是 v_i 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：

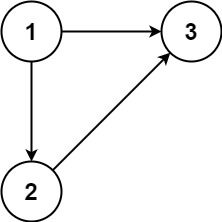
输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]

示例 2：

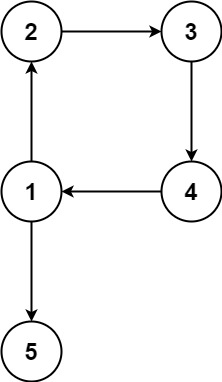
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]

提示：

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= u_i, v_i <= n

相似问题：

0684：冗余连接

分析

显然有根树等价于所有节点连通，且只有一个节点入度为 0，其它节点入度都为 1
输入的图有两种情况：
- 多余的边指向根节点：所有节点的入度都为 1 ，存在一个环，删除环中任意一条边即可
- 多余的边指向其它节点 v：只有节点 v 的入度为 2，应选择一条指向 v 的边删除
因此可以先遍历边，统计入度
- 若有节点 v 的入度为 2，遍历指向 v 的边，假如去掉该边不影响连通性，即可删除
- 若没有节点 v 的入度为 2，转为 0684

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution:
    def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
        def find(x):
            if f[x] != x:
                f[x] = find(f[x])
            return f[x]

        def union(x, y):
            f[find(x)] = find(y)

        def check(u, v):
            for x, y in edges:
                if (x, y) != (u, v):
                    union(x-1,y-1)
            return len({find(i) for i in range(n)})==1

        n = len(edges)
        f, d = list(range(n)), {}
        for u,v in edges:
            if v in d:
                return [u,v] if check(u,v) else [d[v],v]
            d[v] = u
        for u,v in edges:
            if find(u-1)==find(v-1):
                return [u,v]
            union(u-1,v-1)

7 ms

目录

0685：冗余连接 II（★★）

题目

分析

解答