力扣第 675 题
题目
你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示, 在这个矩阵中:
0 表示障碍,无法触碰1 表示地面,可以行走比 1 大的数 表示有树的单元格,可以行走,数值表示树的高度
每一步,你都可以向上、下、左、右四个方向之一移动一个单位,如果你站的地方有一棵树,那么你可以决定是否要砍倒它。
你需要按照树的高度从低向高砍掉所有的树,每砍过一颗树,该单元格的值变为 1(即变为地面)。
你将从 (0, 0) 点开始工作,返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树,返回 -1 。
可以保证的是,没有两棵树的高度是相同的,并且你至少需要砍倒一棵树。
示例 1:

输入:forest = [[1,2,3],[0,0,4],[7,6,5]]
输出:6
解释:沿着上面的路径,你可以用 6 步,按从最矮到最高的顺序砍掉这些树。
示例 2:
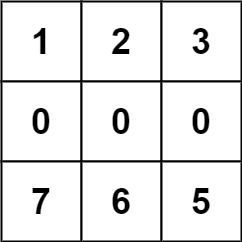
输入:forest = [[1,2,3],[0,0,0],[7,6,5]]
输出:-1
解释:由于中间一行被障碍阻塞,无法访问最下面一行中的树。
示例 3:
输入:forest = [[2,3,4],[0,0,5],[8,7,6]]
输出:6
解释:可以按与示例 1 相同的路径来砍掉所有的树。
(0,0) 位置的树,可以直接砍去,不用算步数。
提示:
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109
分析
从低到高依次 bfs 找树即可,可以预处理每个格子能移动的方向,优化速度
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution:
def cutOffTree(self, forest: List[List[int]]) -> int:
def bfs(s,e):
Q, vis = [(0,s)], [0]*(m*n)
vis[s] = 1
for w,u in Q:
if u==e:
return w
for v in g[u]:
if not vis[v]:
vis[v] = 1
Q.append((w+1,v))
return inf
F = forest
m, n = len(F),len(F[0])
d, g = {}, defaultdict(list)
for i in range(m):
for j in range(n):
c = F[i][j]
if c==0:
continue
if c>1:
d[c] = i*n+j
for x,y in [(i+1,j),(i,j+1)]:
if 0<=x<m and 0<=y<n and F[x][y]:
g[i*n+j].append(x*n+y)
g[x*n+y].append(i*n+j)
res,u = 0,0
for c in sorted(d):
v = d[c]
w = bfs(u,v)
if w==inf:
return -1
res,u = res+w,v
return res
|
1735 ms
*附加
- 也可以用 A* 启发式路径算法,类似于 dijkstra,不过添加了一个估算权重 aw
- 估算权重一般取理论上的最小值,本题中两个格子的理论最短距离即是曼哈顿距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution:
def cutOffTree(self, forest: List[List[int]]) -> int:
def astar(s,e):
def f(v):
a1,b1 = divmod(v,n)
a2,b2 = divmod(e,n)
return abs(a1-a2)+abs(b1-b2)
pq,d = [(f(s),0,s)], [inf]*(m*n)
d[s] = 0
while pq:
aw,w,u = heappop(pq)
if u==e:
return w
for v in g[u]:
if w+1<d[v]:
d[v] = w+1
heappush(pq,(w+1+f(v),w+1,v))
return inf
F = forest
m, n = len(F),len(F[0])
d, g = {}, defaultdict(list)
for i in range(m):
for j in range(n):
c = F[i][j]
if c==0:
continue
if c>1:
d[c] = i*n+j
for x,y in [(i+1,j),(i,j+1)]:
if 0<=x<m and 0<=y<n and F[x][y]:
g[i*n+j].append(x*n+y)
g[x*n+y].append(i*n+j)
res,u = 0,0
for c in sorted(d):
v = d[c]
w = astar(u,v)
if w==inf:
return -1
res,u = res+w,v
return res
|
3587 ms

